正100角形は作図できませんけど。 数学的にどうこうというよりは単にめんどうくさい作業がだらだらつづきます。 一部については、コンパスと定規だけで作図を行う手順とその証明をPDFファイルにしました。 作図の過程を示すhtml5canvasアニメ・動画は作図可能なものすべてについて、作成していきます。 頂点の個数が奇数の素数で作図可能なものを(2) 線分abを底辺とする正三角形の頂点cを求める。 (3) 円弧obを6等分して,各等分点を1,2,・・・,5とする。 (4) c1=coとなるように,点oを求める。 (5) 点oを中心とし,点a及び点bを通る円は正7角形の外接円となるので,正7角形の頂点が求まる。 · クイズとかの類ではないのですが、一辺の長さが決まっている正五角形を定規とコンパスだけで書くことは出来るのでしょうか。(仮に一辺を30mmとします) 過去にも類似質問がありましたので,そちらも御覧になって見て下さい。 ・http/

コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
十角形 書き方
十角形 書き方-正五角形は星を五角形で表すように端正な形ですね。 でも、正五角形を描いてというと、多くの方が「うーん!ちょっと待って」となります。 まして、正七角形をとなれば「勘弁してよ!」ではありませんか。 ならばと、正多角形の描き方を紹介します。HOME よみもの 正多角形 正10角形 正五角形を作図する要領で円周の五分の一を作図します。 その半分が作図できれば完了です。




機械設計のための基礎製図
課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心をって正六角形の頂点を決めて作図をしていました。 その後は,なぜコンパスだけで正六角形がかけるか という説明活動(算数的な活動)を行い,筋道を立て る考え方を育てました。 さて,正三角形,正方形,正六角形,正八角形がで黄金三角形は,正五角形(後述)や図6 の正十角 形の中にも現れ,それらの図形においても黄金比が 密接に関係している. 4.正五角形と黄金比 図7 のような正五角形(pentagon)において,対 角線を全て描くと,五芒星(pentagram)が得られ る.
· 6 1123 まずは正六角形を書きます。 使用するのはコンパスと定規。 コンパスで円を書き、任意の円周上の一点に針を置き、 円を描いた半径を保ったまま更に円を描きます。 この時、円全体を描くのではなく、元々の円と交差する部分だけを描きます。 その点を中心に更に同じことを繰り返すと、円周上に等間隔に6つの点が打てます。 それを結べば正六角点の結び方 星形五角形 星形六角形 星形七角形 星形八角形 星形九角形星形十角形 角の和の公式 単位:度(°) 180° 360° 540° 7° 180° 360° 540° 180° 360° 7° 900° 1080° 180n-360×2 =180(n-4) 180n-360×3 =180(n-6) 180n-360×4 =180(n-8) p番目 ごと 180n-360・星形七角形は1点とばしと2点とばしで2つできることに気づいた生徒は数人。 ・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。
円に内接する正多角形 にリンクを張る方法 ホーム円に内接する多角形を書くには。 幾つか方法はあると思いますが。 多角形コマンドを使うのが簡単だと思います。 操作方法 多角形 -角数を入力 -寸法は無指定 -円上にマウスポインタを合わせて 右ドラッグ+3時の方向 中心点・a点と表示されたらはなす · スクラッチ30(Scratch)を使って、円・多角形やアートをかこう 年から小学校の学習において「プログラミング教育必修化」も決定しておりますが、学校ではいったいどのような授業がされるのでしょうか? 「小学校プログラミング教育の手引(第二版




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




驚くばかり正 五角形 書き方 簡単 最高のぬりえ
星型多角形とは,一般的な多角形とは異なり特 殊な形をしているが,見方を変えることで両者の 関係性が明らかになった。 (4) 星型多角形の内角の和の求め方 ることは,多角形を三角形に分割することで演繹 的に示すことができる。では,星型多角形も同様コンパスを使って描いた円を基準にして正五角形をを描く方法です。 ☆用具:直線定規、コンパス (1) 基準となる直線上の点Oを中心に円を描き、円と直線の交点ABを求める。 (2) コンパスを使い、点Aを中心にAOと同じ長さを半径とする弧を描き、 交点EFを求める。 点E、Fを結んで、直線ABと垂直になる線を描き、直線ABとの交点Gを求める。 (3) 点Gを中心に直線CGの長・垂線を作図する。(正方形) ・あとは同様に行う。 (3)5の倍数の正多角形 (正五角形、正十角形、正二十角形、正四十角形) ・(1)、(2)と同様に行う。 ※基本の作図を使うとほぼ、正多角形の作図ができることに注目させたい。 授業コンセプト




小5 算数 小5 33 五角形 六角形 多角形 Youtube




Images Of 十七角形 Japaneseclass Jp
以下を求めよ (1)半径1 の円に外接する正六角形の面積 (2)半径1 の円に内接する正十角形の1 辺の長さ (3)放物線y = x2 上の2 点P(a;a2), Q(b;b2) がb = a2 を満たしながら動くと する · まず初めに、定規で書く正五角形の書き方を紹介します。使用する用具は定規と筆記用具だけという手軽さです。用具がそろっていない場合におすすめです。 書き方の手順<前半> ・手順1:最初に、線分abを引きます。 ・手順2:線分abの中点mをとります。形 なし なし なし 四 角 形 なし なし なし 五 角 形 なし なし 六 角 形 なし なし 七 角 形 なし 八 角 形 なし 九 角 形 十 角 形 活動σ規則性を見つけ、式に表す。 ※m 点とばし星型n 角形の内角の和は180°×(n-2-2m)と表すことができる。 180° 360° 540
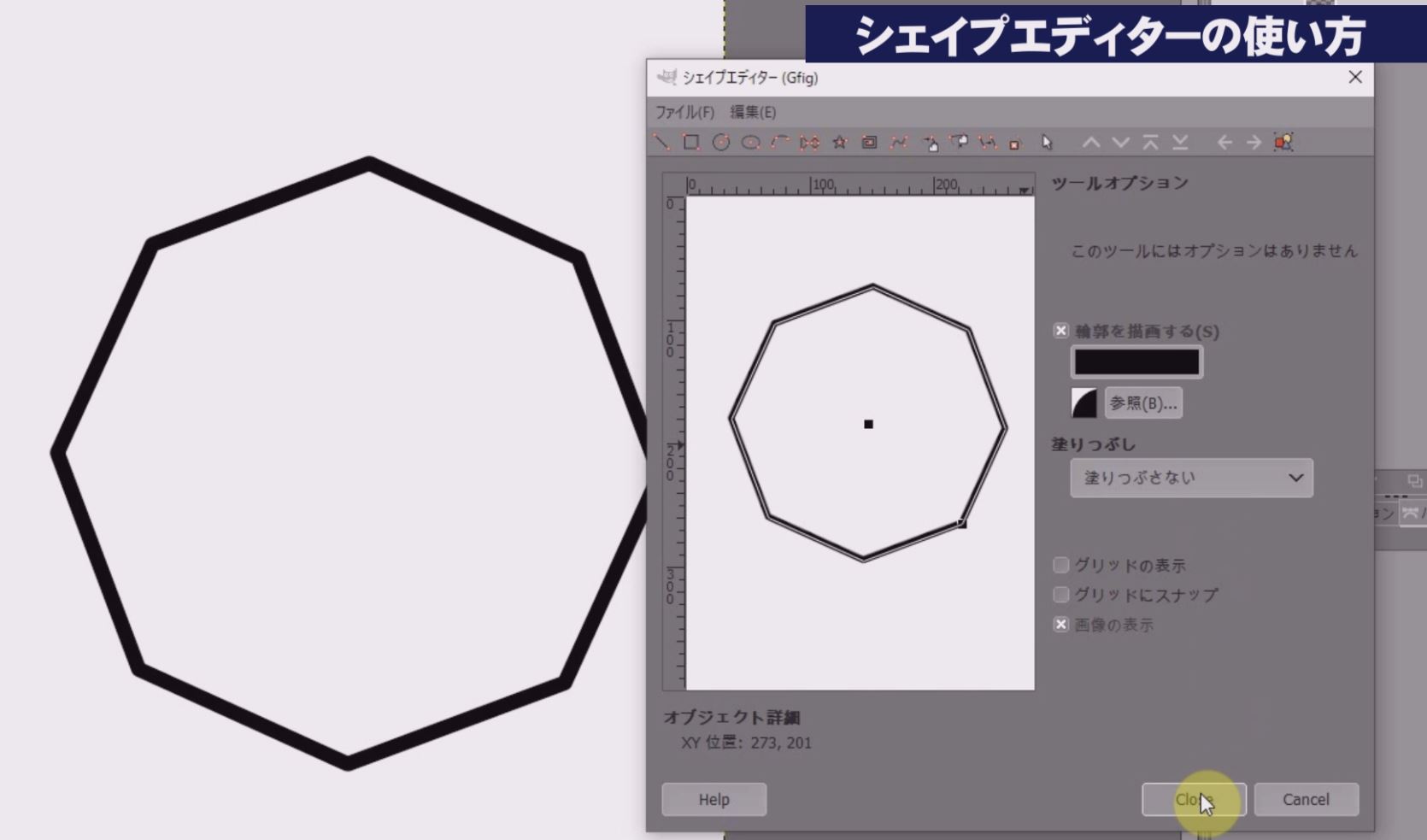



Gimpで楕円形や多角形の図形をシェイプエディターでの作成する使い方
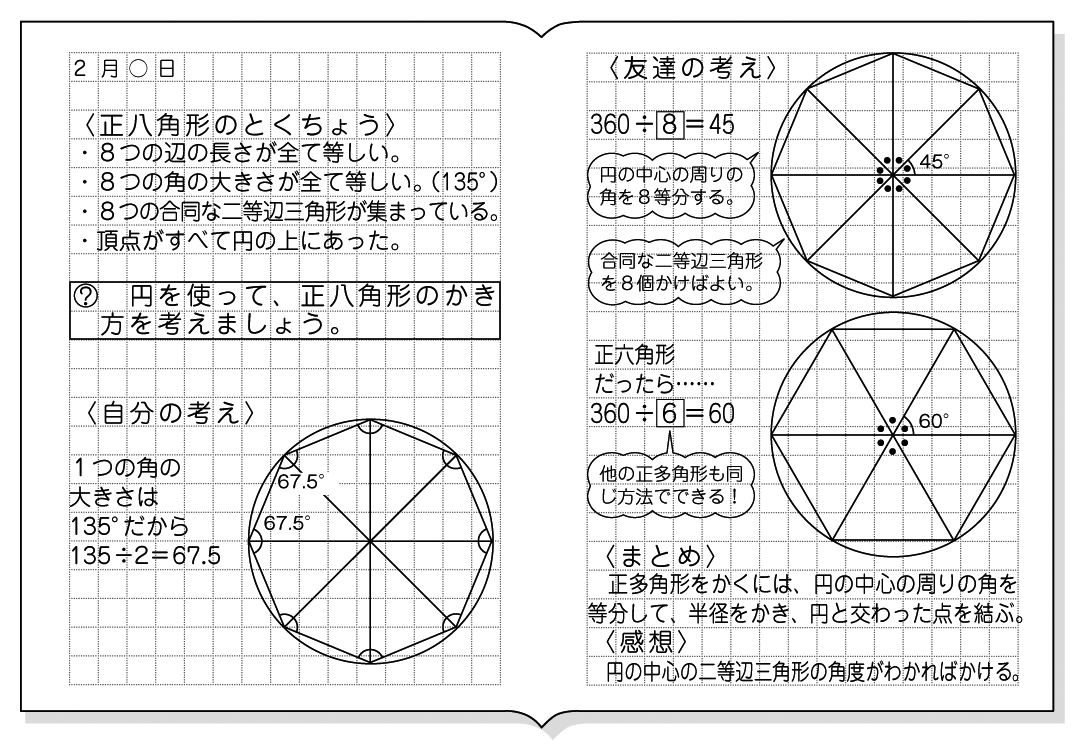



小5算数 正多角形と円 指導アイデア みんなの教育技術
· 正八角形の書き方 まずは正方形を書きます 次に対角線を書きます 対角線の交点と四角形の頂点を半径とする円の弧を書き正方形との交点を出します 四角形の頂点全てから同じように弧を書き、交点を出します 隣り合う交点を直線で結んでいくと正八角形が出来ます! 手順まとめ ついでに正六角形の書き方も まずはコンパスで円を書きます正十角形 書き方 簡単 黄金比矩形および内接正五角形、正十角形の描き方 Decago 拙著『ヴァイオリンのf孔』より 1 正方形(縄と結び目によるの作図) 作りたい正方形の一辺となる長さ230m(例として、クフ王の第一ピラミッドで考える)に杭を打ち縄を張る。証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説! 正三角形の角度 正方形、ひし形との融合問題を解説!
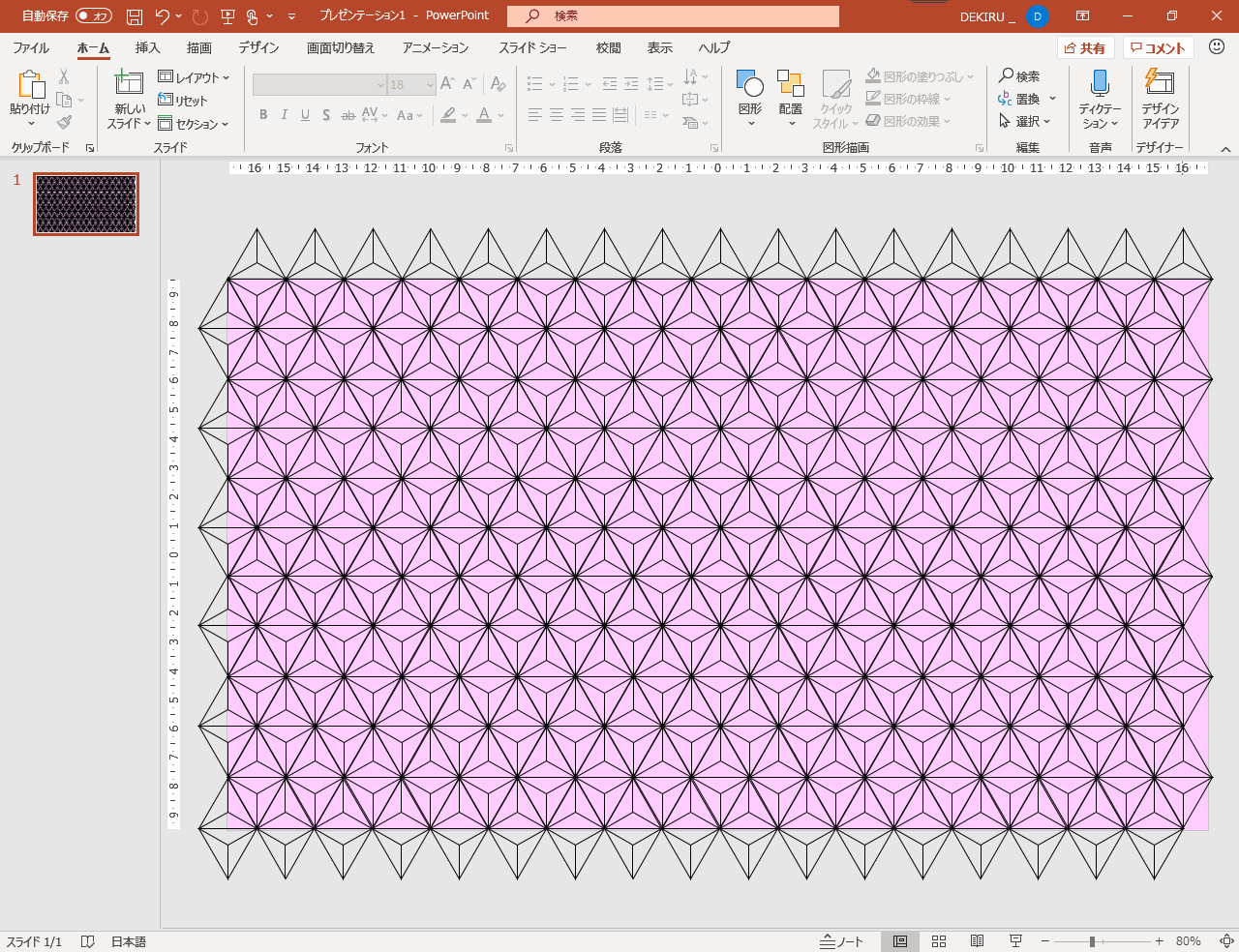



Powerpointの図形で 麻の葉模様 を描く方法 ひし形と直線で基本パーツを作ろう できるネット




3月30日は正十七角形が定規とコンパスだけで作図可能なことが発見された日です ニュートンのオレンジの木
· eテレ「デザインあ」の『もん(紋)』をみた方で 自分でも描いてみたいな。 どこかに書き方がないかな。 と探している方のために、今回は書き方のプリントをご紹介します。 色紙で紋を作りたい方は下記をご覧ください。 // 紋「梅の花」の書き方プリント 天神様とかかわりの深い「梅の · 正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる! 正多角形の内角の公式 正多角形の1つの内角の大きさを求めたいときは、 つぎの公式をつかってみて。 正n角形の1つの内角は、 · 半円もしくはパイやピザをカットしたような図形は arc () を使って描けます。




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




円を利用して正多角形をかく方法 算数の自主学習 家庭学習レシピ
· 系列が後ろ側に隠れてしまって選択できない場合は、グラフが選択されている状態で、 書式タブ → グラフの要素の をクリック して、 表示された一覧から、 系列〇〇を選ぶ と、 それぞれの系列(色を透明にする部分)を選択することができます 。 選択したら、右側の作業ウィンドウで 塗りつぶしと線の、マーカーに移動して、塗りつぶし(単色)に · エクセルで正多角形を描く方法を教えて下さい。 「挿入」タブの「図形」の中には3,4,5,6,7,8,10,12角形しかないようです。それ以外の正多角形を正確に描く方法を教えて下さい。 11角形・・・・・「A1」~「A11」に、1、と入力⇒範囲選択⇒グラフウイザード⇒グラフの種類、「レーダー」⇒完了11十六角形(じゅうろくかくけい、じゅうろっかっけい、hexadecagon)は、多角形の一つで、16本の辺と16個の頂点を持つ図形である。 内角の和は25°、対角線の本数は104本である。 正十六角形においては、中心角と外角は225°で、内角は1575°となる。 一辺の長さが a の正十六角形の面積Sは



十角形 Wikipedia




平面図形の英語表現一覧 丸 三角 長方形 正方形など 30代40代で身につける英会話
十角形(じっかくけい、じっかっけい、英 decagon )は、多角形の一つで、10本の辺と頂点を持つ図形である。 内角の和は1440°、対角線の本数は35本である。 正十角形においては、中心角と外角は36 °で、内角は144°となる。 一辺の長さが a の正十角形の面積 S は、 = =この方法は正五角形の外接円が書けるので、正十角形や正十五角形、正二十角形へと発展していく作図法です。 第1法では外接円が書けないので、このような発展はできません。 正六角形の作図 正6角形。書き方はいちばんシンプルですね。九角形 (きゅうかくけい、きゅうかっけい、英:nonagon、enneagon)は、 多角形 の一つで、 9 本の 辺 と9個の 頂点 を持つ 図形 である。 内角 の 和 は 1260 °、 対角線 の本数は27本である。 正九角形においては、 中心角 と 外角 は 40 ° で、内角は140°となる。 一辺の長さがaの正九角形の 面積 Sは、 S = 9 4 a 2 cot π 9 ≃ 6181 a 2 {\displaystyle S= {\frac {9} {4}}a^ {2}\cot {\frac




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




正多角形をプログラミングで描く意味 その先にあるのは 考えることを考える力 バレッドプレス Valed Press
· 正十角形の書き方 (美しく描くと発見も多い! ) で、「どうやって作図するんですか? 」って聞かれたので、 ひだまりママが描いた方法を紹介しておきまーす。 あとは、下の手順。 ちょっと見くかったらごめんね! これ見てわかんないけど、描きたい!
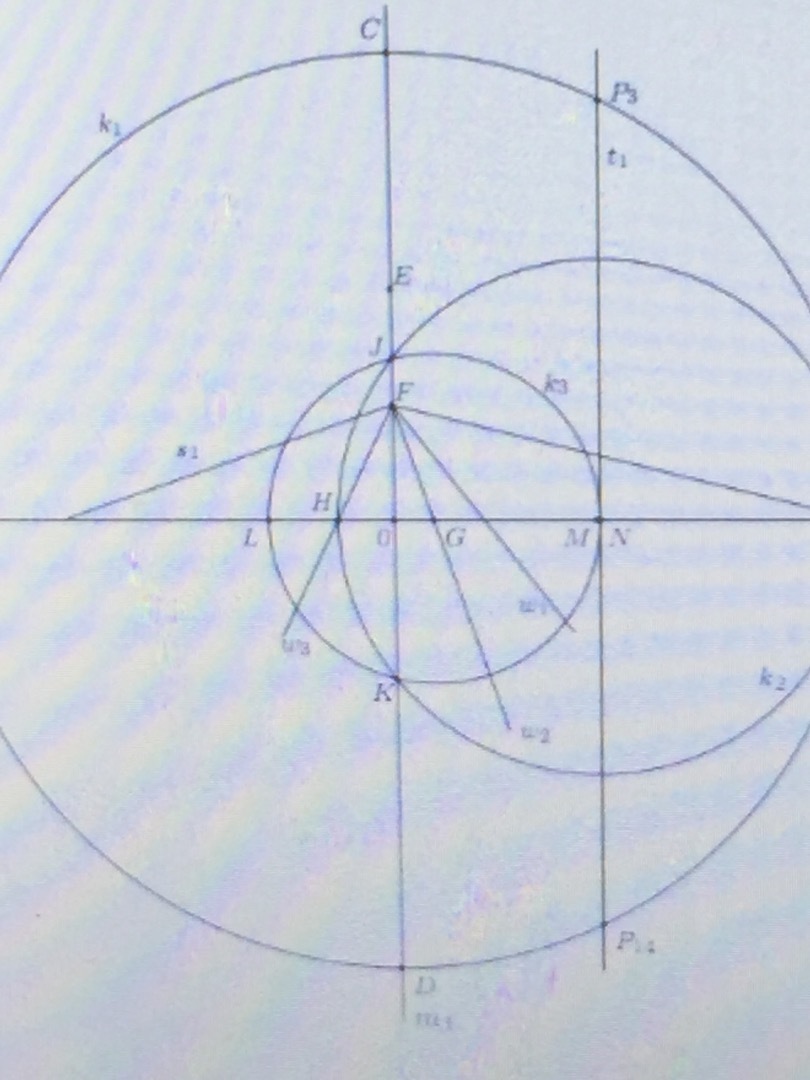



角形が作図できることを示した 数学者 原聡志のブログ マニアック人物図鑑



五角形



正七角形は線対称ですか 点対称ですか 奇数の正多角形は線対称 偶数の正 Yahoo 知恵袋
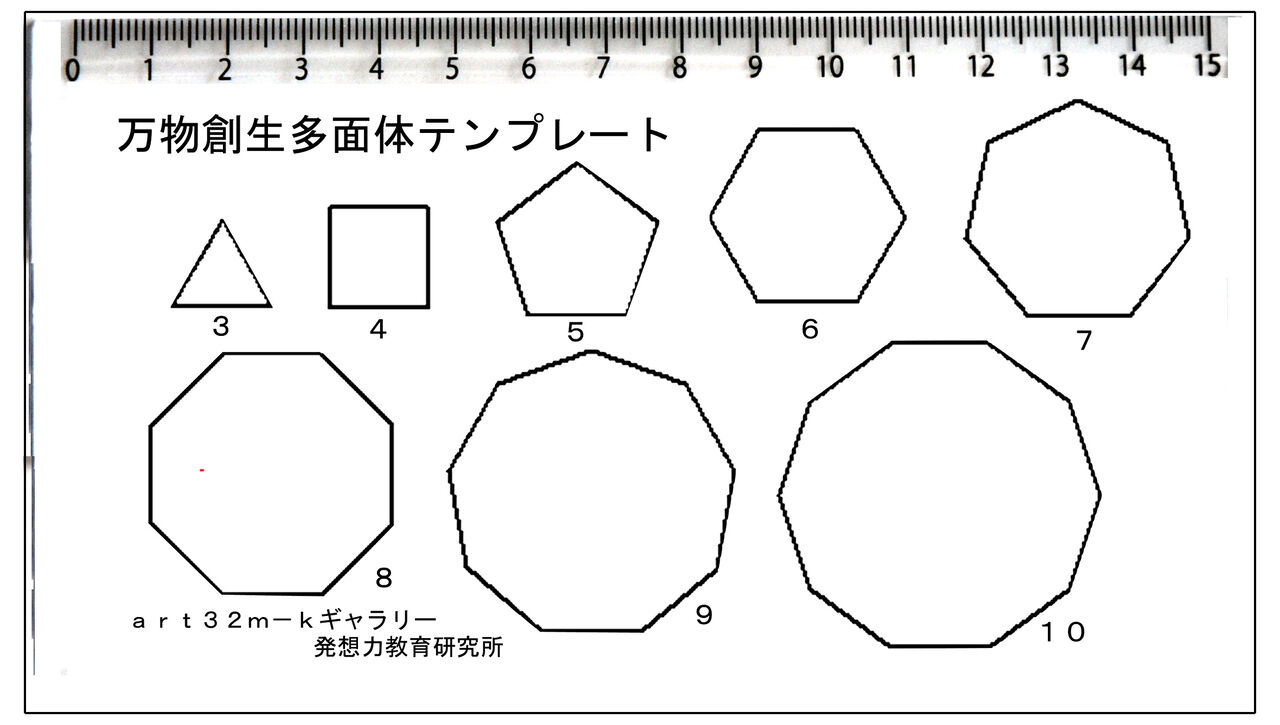



正5角形の積木箱 ペンタゴンデカゴンフラワー定理 倍角数定理 発想力教育研究所 素数誕生のメカニズム
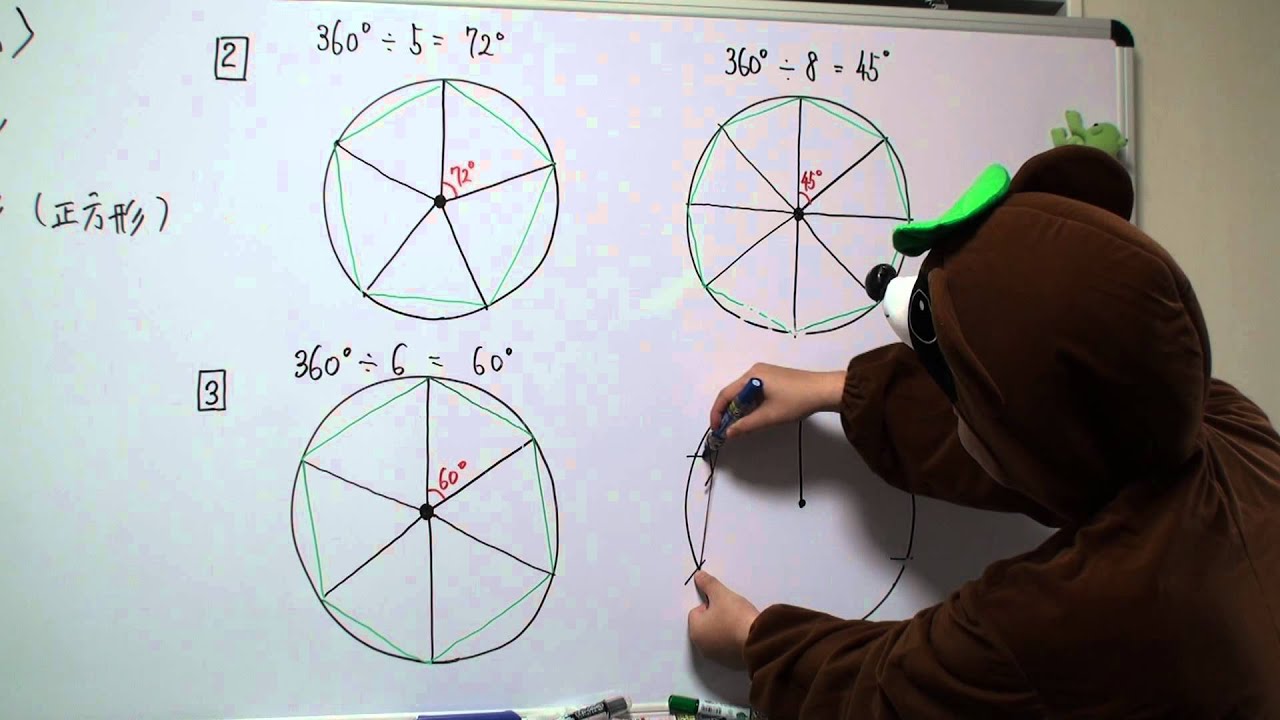



小5算 多角形と円8 宿題解説 かいせつ 円の中にコンパスで正6角形を作図 Youtube




Images Of 十角形 Japaneseclass Jp




正5角形の積木箱 ペンタゴンデカゴンフラワー定理 倍角数定理 発想力教育研究所 素数誕生のメカニズム



正9角形 に関するq A Yahoo 知恵袋
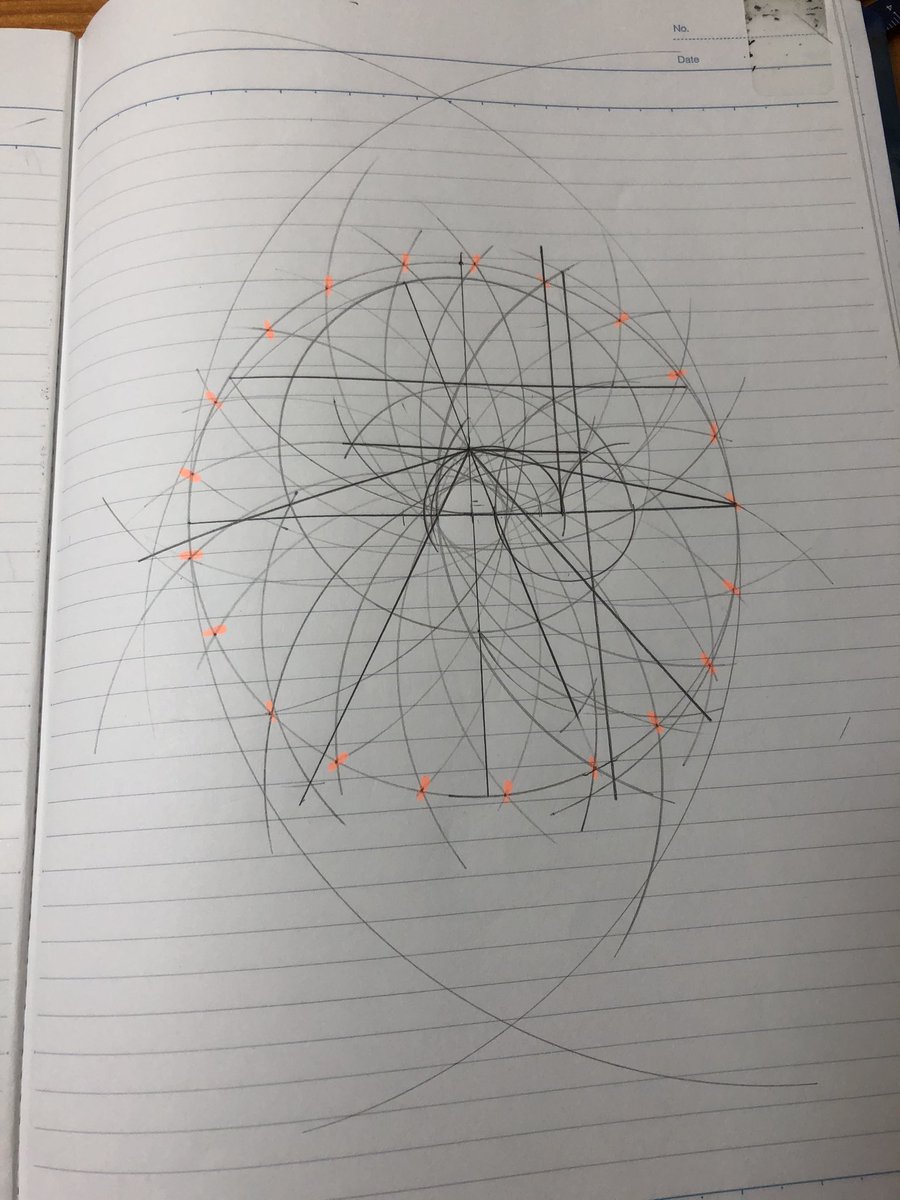



静岡高校数学同好会 V3 2 Unofficial No Twitter あ ありのまま 今 起こった事を話すぜ おれは 正17角形を作図していたと思ったら 21角形になっていた




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




正十角形の書き方 ひだまりママのブログ




Images Of 十角形 Japaneseclass Jp
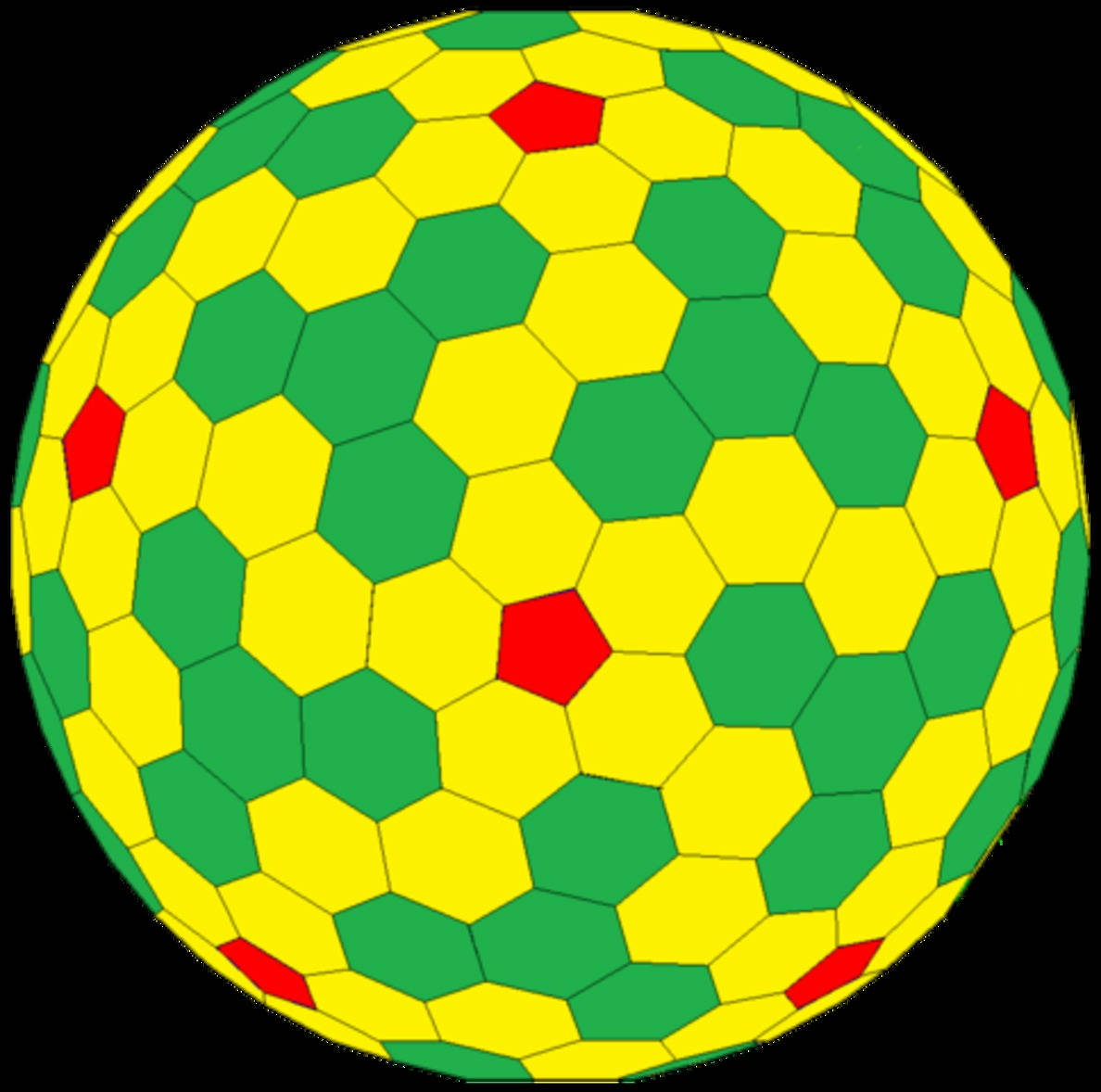



400年ぶりに新種の 対称性多面体 構造が発見される Gigazine




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




正多角形の作図法 角の三等分と三次方程式の解法 髙木 清 本 通販 Amazon
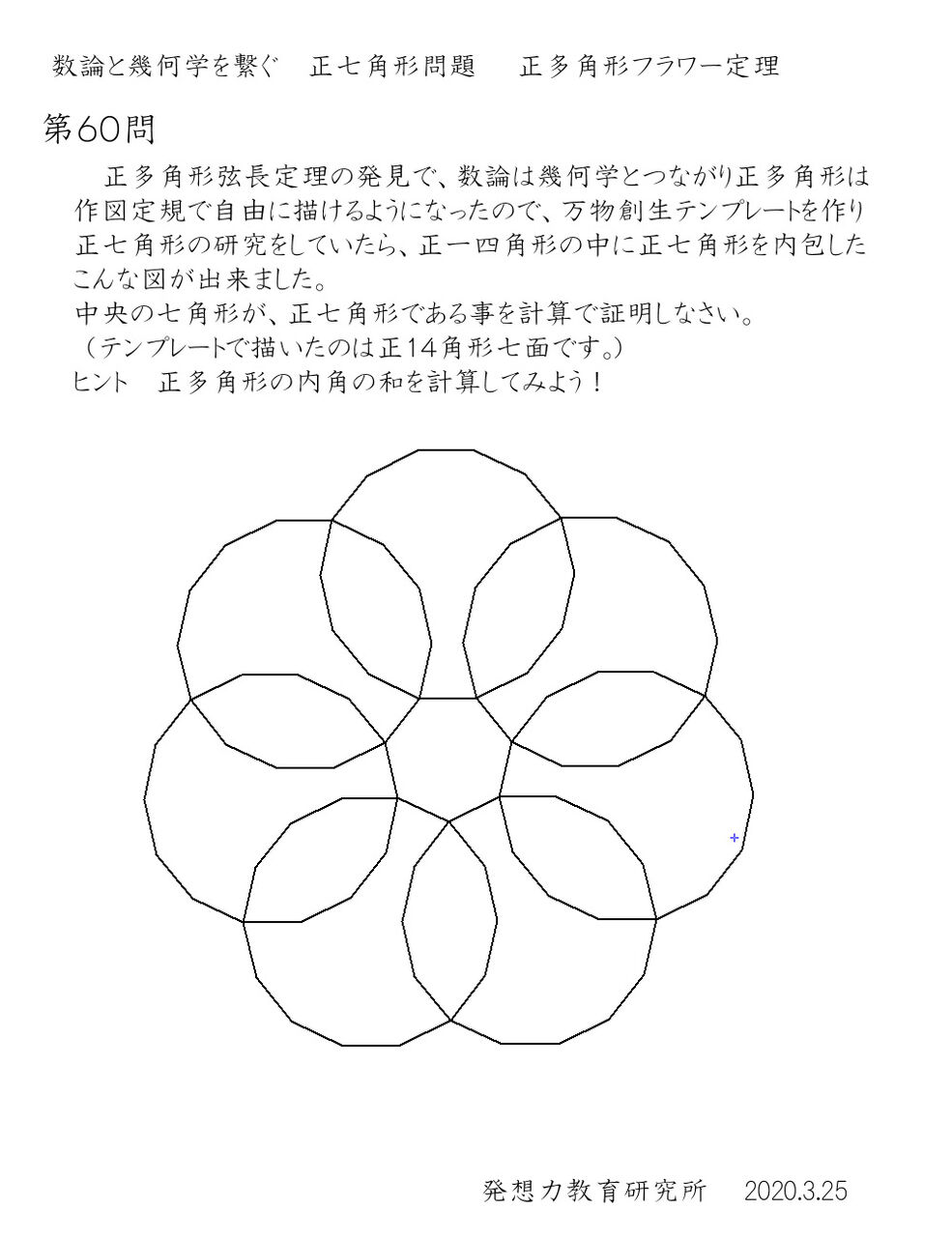



フラクタル自然数1の定義で可視化する正多角形の法則性 発想力教育研究所 素数誕生のメカニズム




Images Of 六万五千五百三十七角形 Japaneseclass Jp
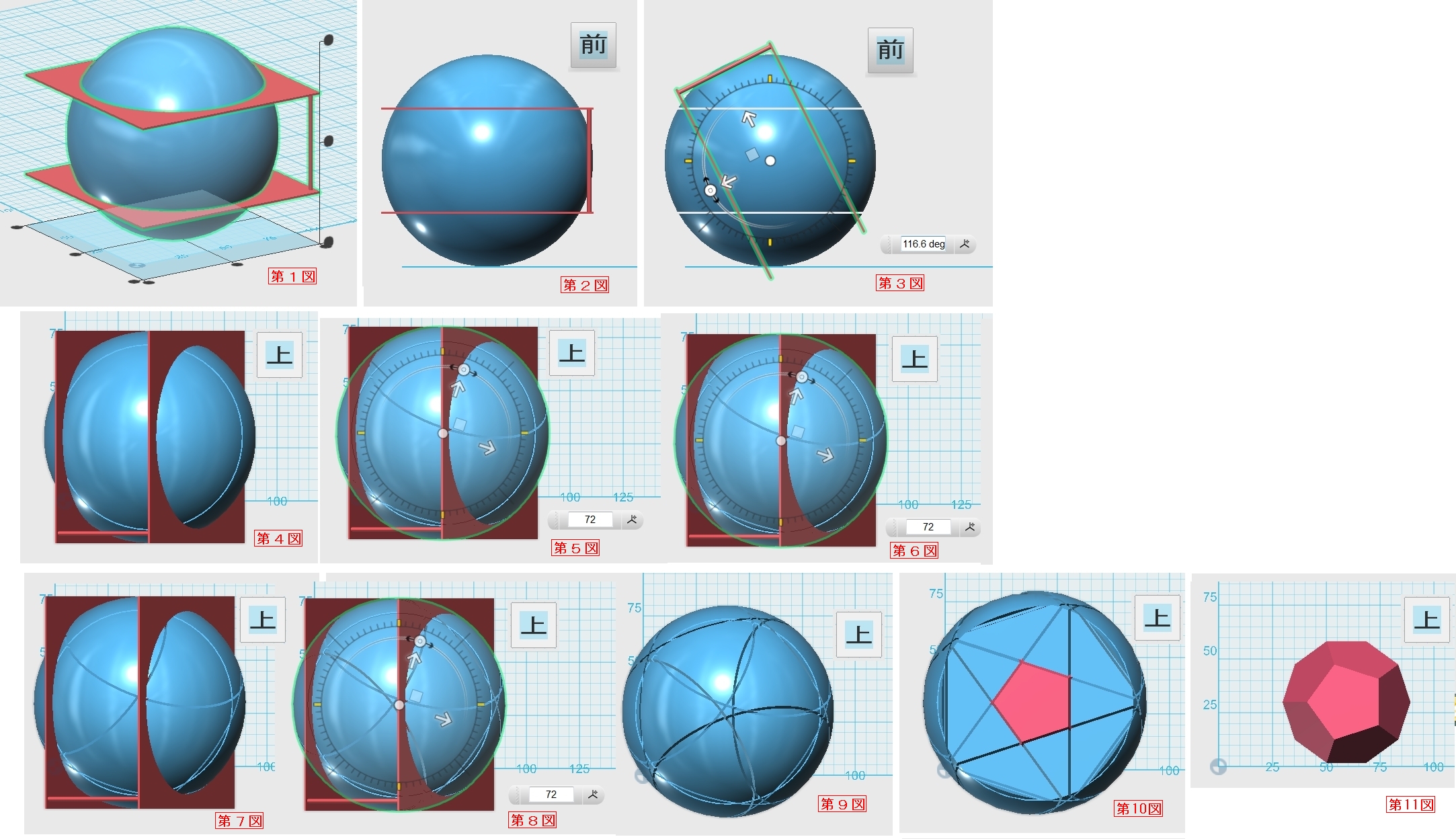



正十二面体のモデリングについて Autodesk Community International Forums




数学で作図不可能と証明された正七角形を描く方法 立体魔方陣 クリプトグラム33 発想力教育研究所 素数誕生のメカニズム



数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog



Idan Tal




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




Viscuit 正十角形作図 Youtube




正多角形の1つの内角 外角を求める方法を問題解説 数スタ




新しい算数 2年度用 小学校教科書のご紹介 東京書籍




六万五千五百三十七角形 Wikipedia




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
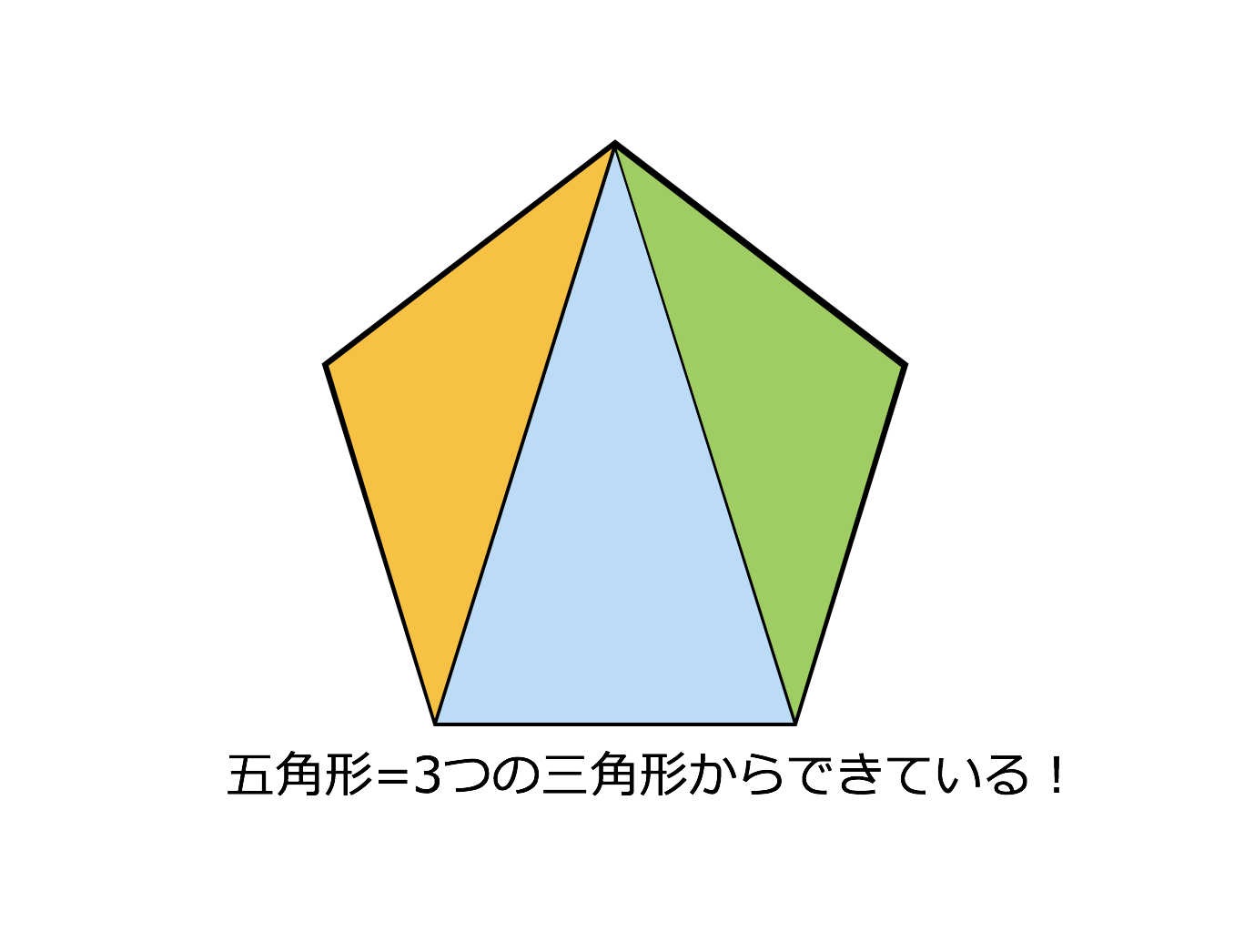



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



黄金比矩形および内接正五角形 正十角形の描き方
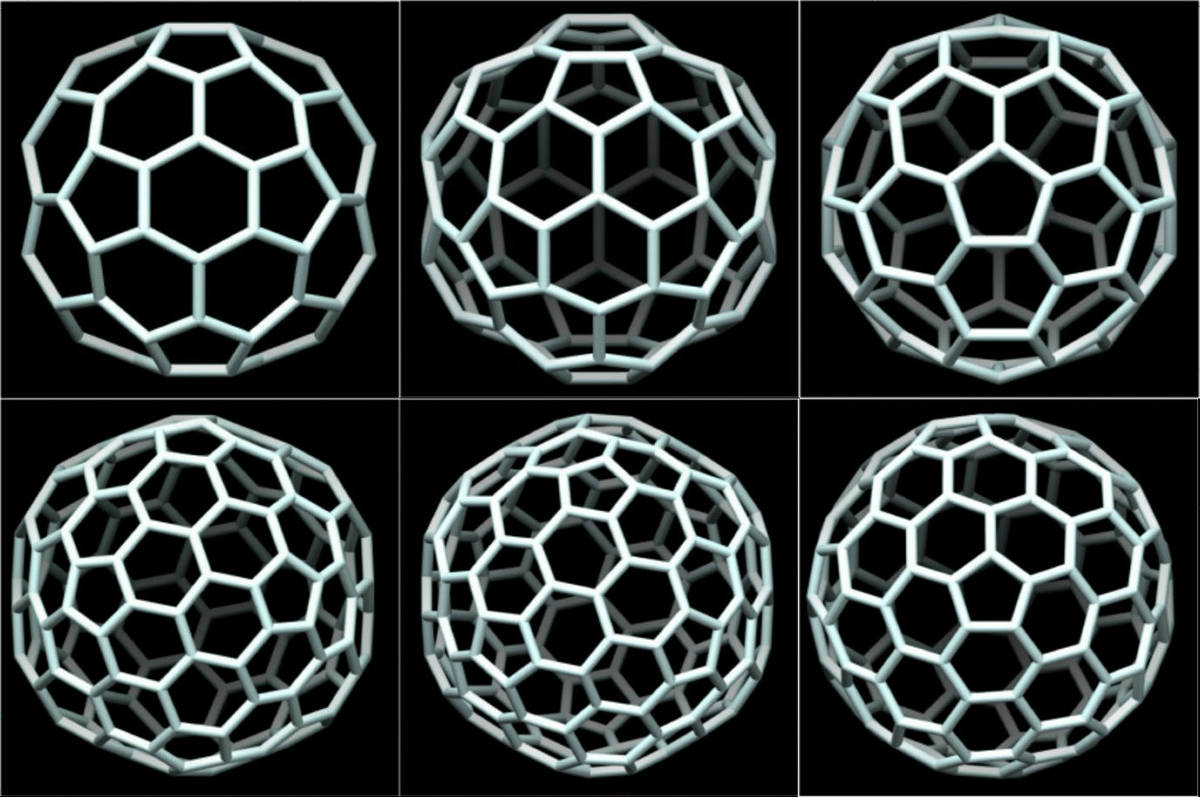



400年ぶりに新種の 対称性多面体 構造が発見される Gigazine




正多角形を定規だけで描く 交点座標から線で結ぶ方法 Alumania Information




機械設計のための基礎製図




発展 正17角形の作図 雲孝夫 Note




正多角形の1つの内角 外角を求める方法を問題解説 数スタ
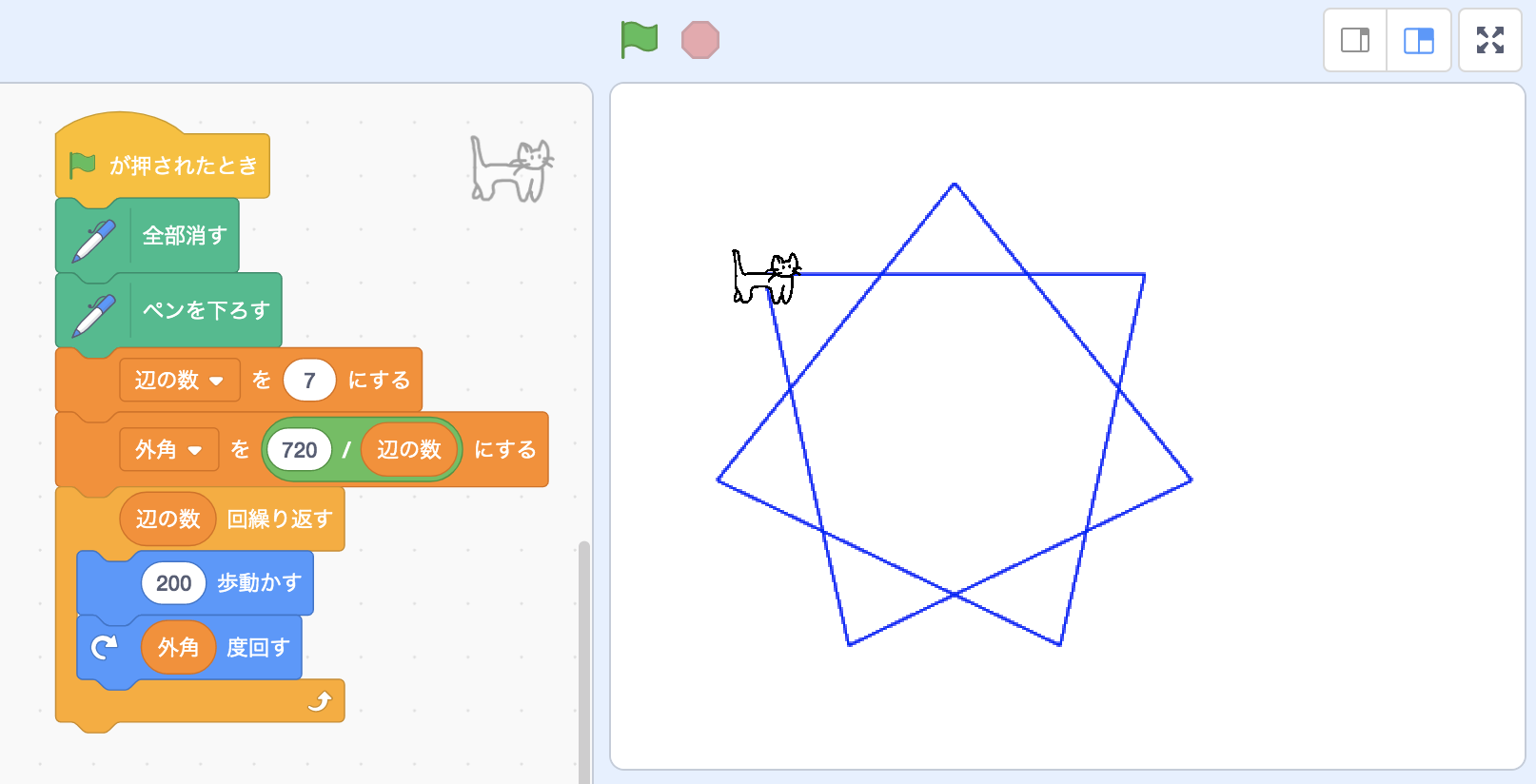



例題 ペンで図形を描画する プログラミング教育のためのスクラッチ例題集
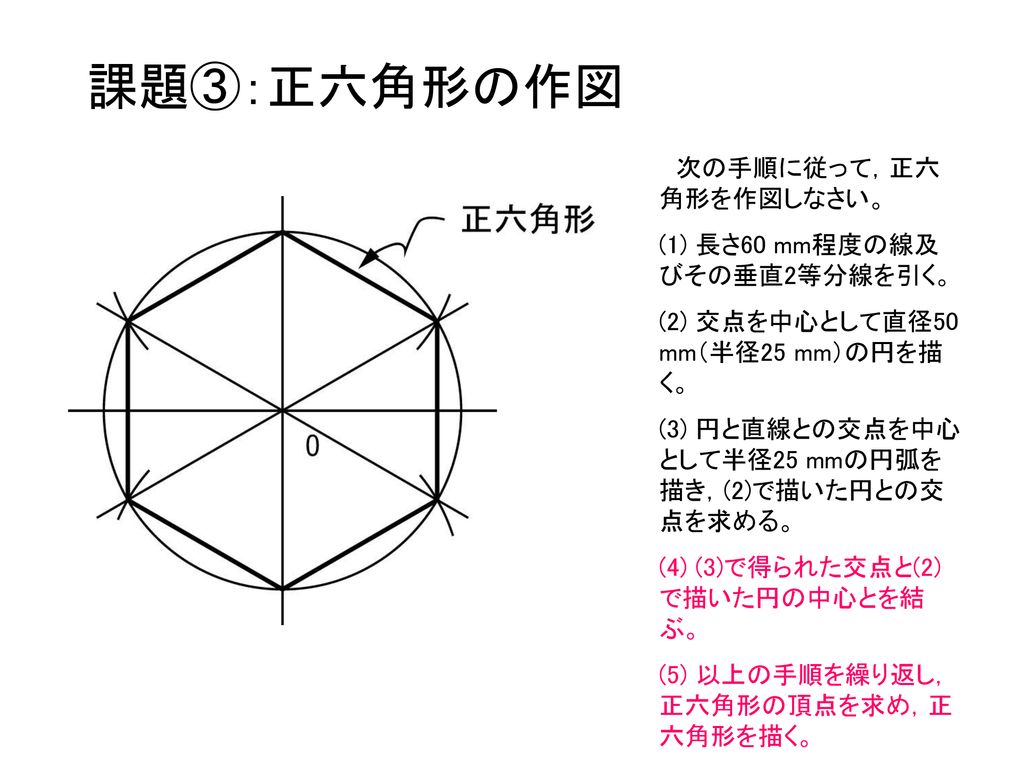



第3回 基礎作図 基本的な作図法をしっかりと学ぶ 本日の課題 Ppt Download
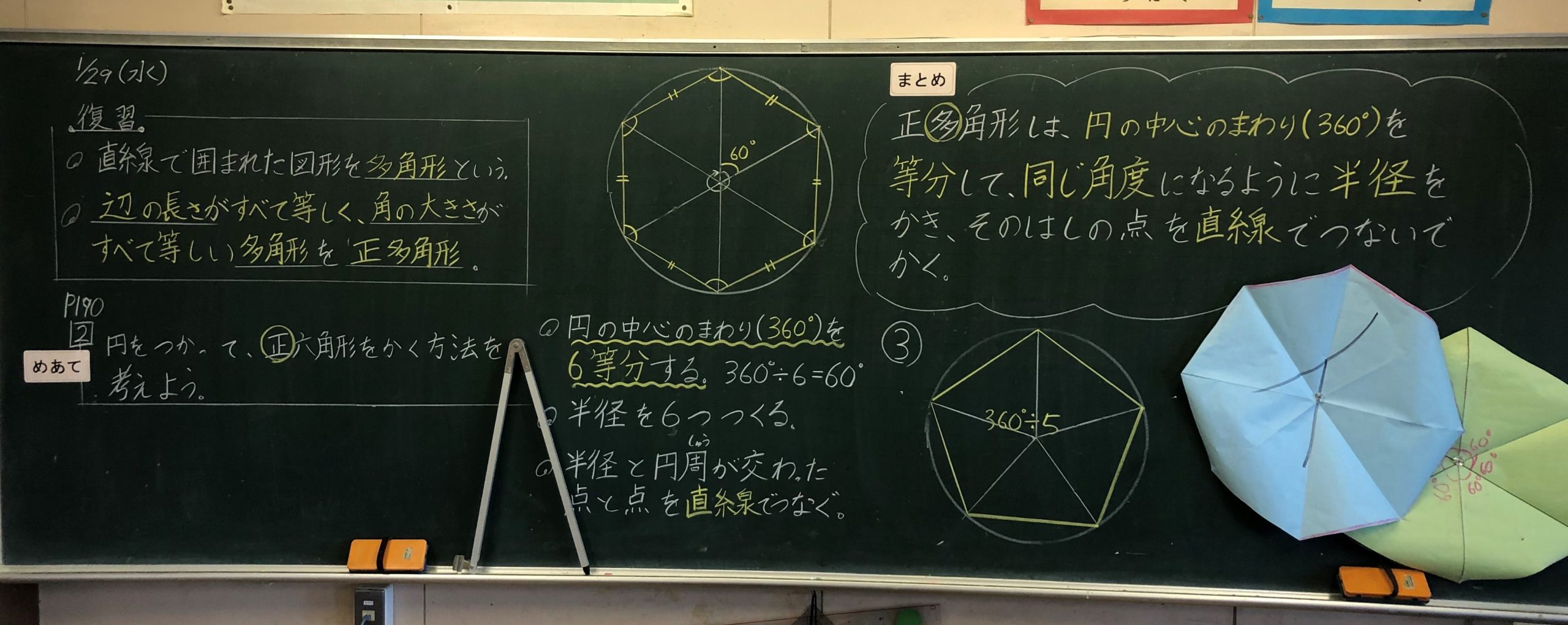



5年生算数 円と正多角形 黒板log 黒板log




Images Of 十七角形 Japaneseclass Jp



黄金比矩形および内接正五角形 正十角形の描き方
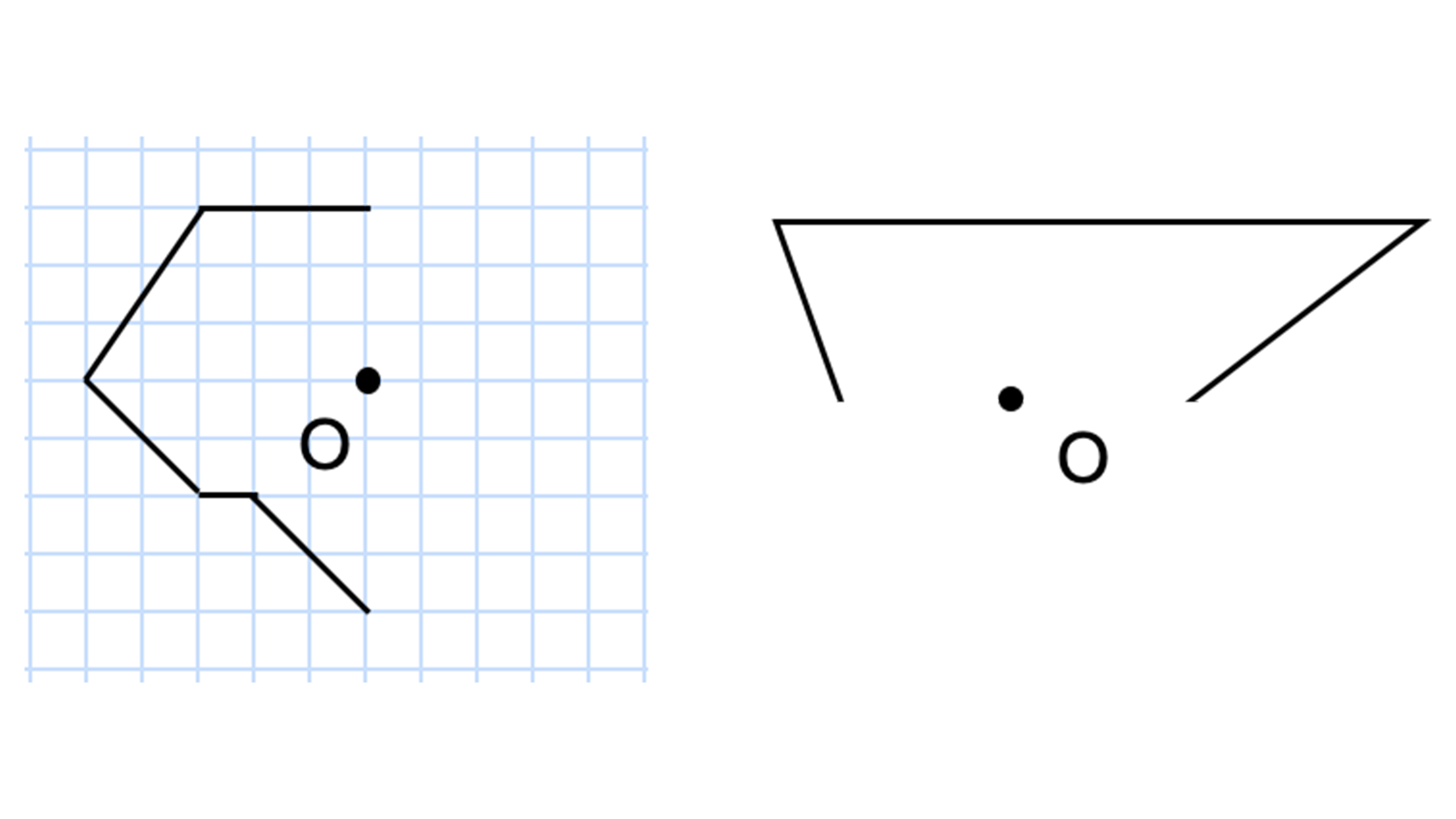



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




二十角形 Wikipedia
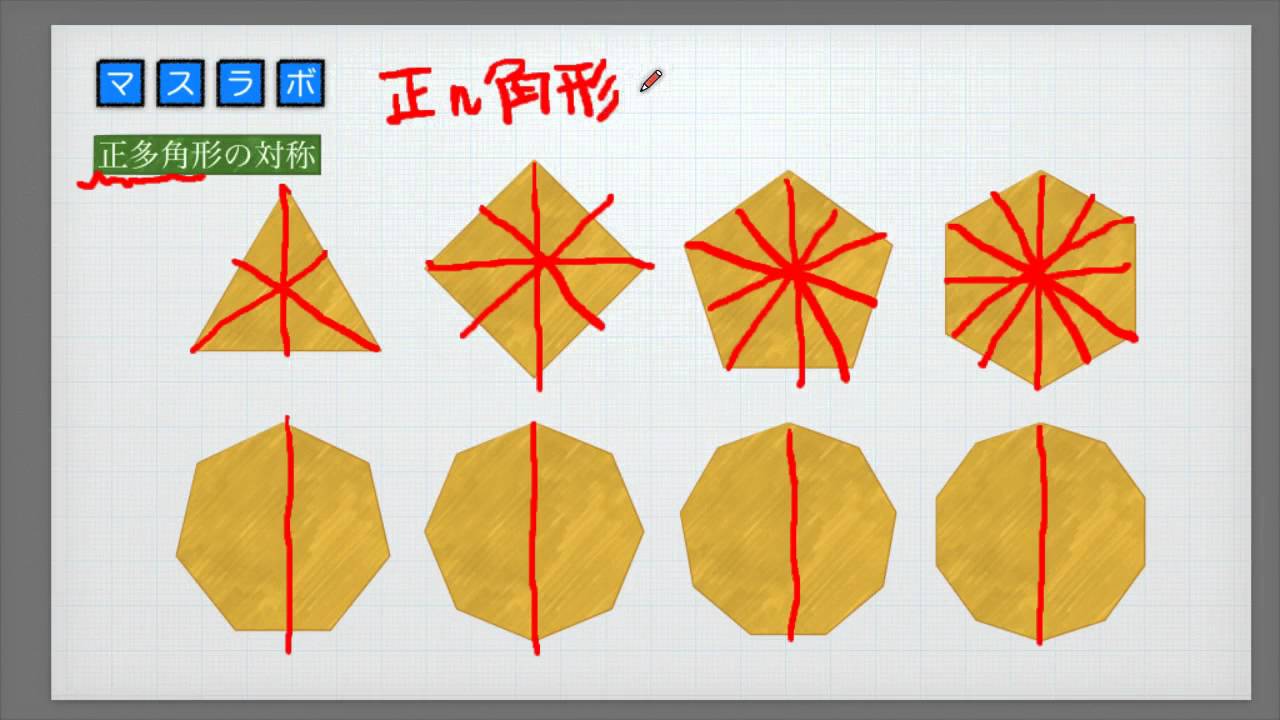



小学校6年生 算数 正多角形の対称 Youtube
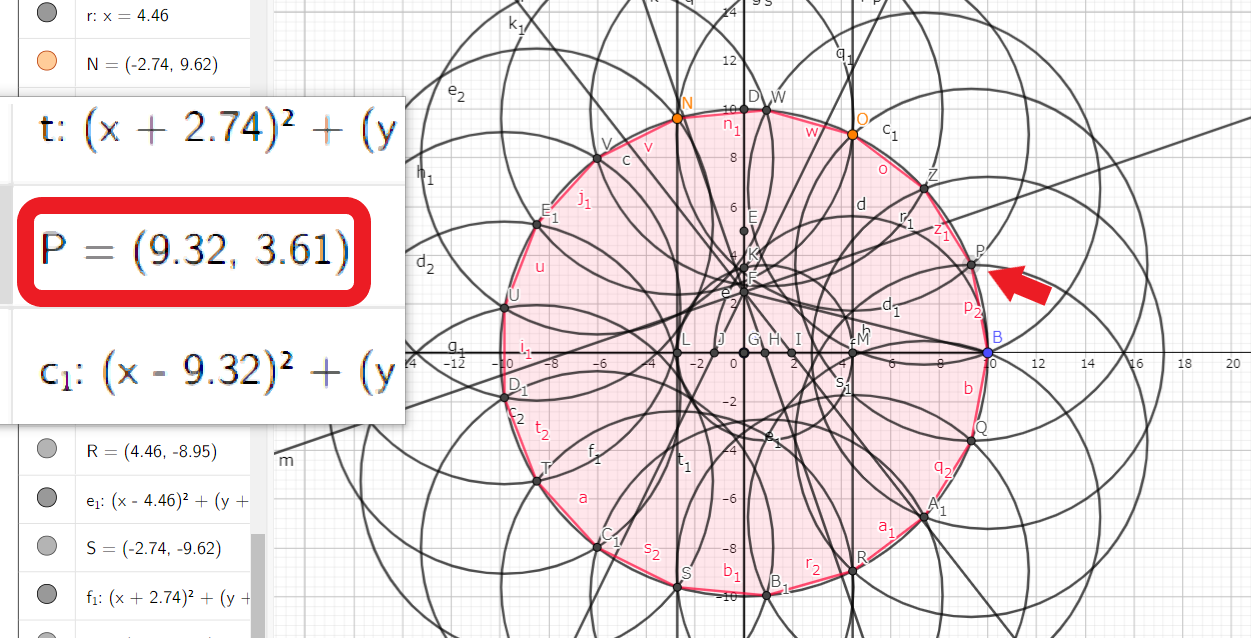



正17角形の作図 Cos 2p 17 の値と作図の関係 Kobayashika64
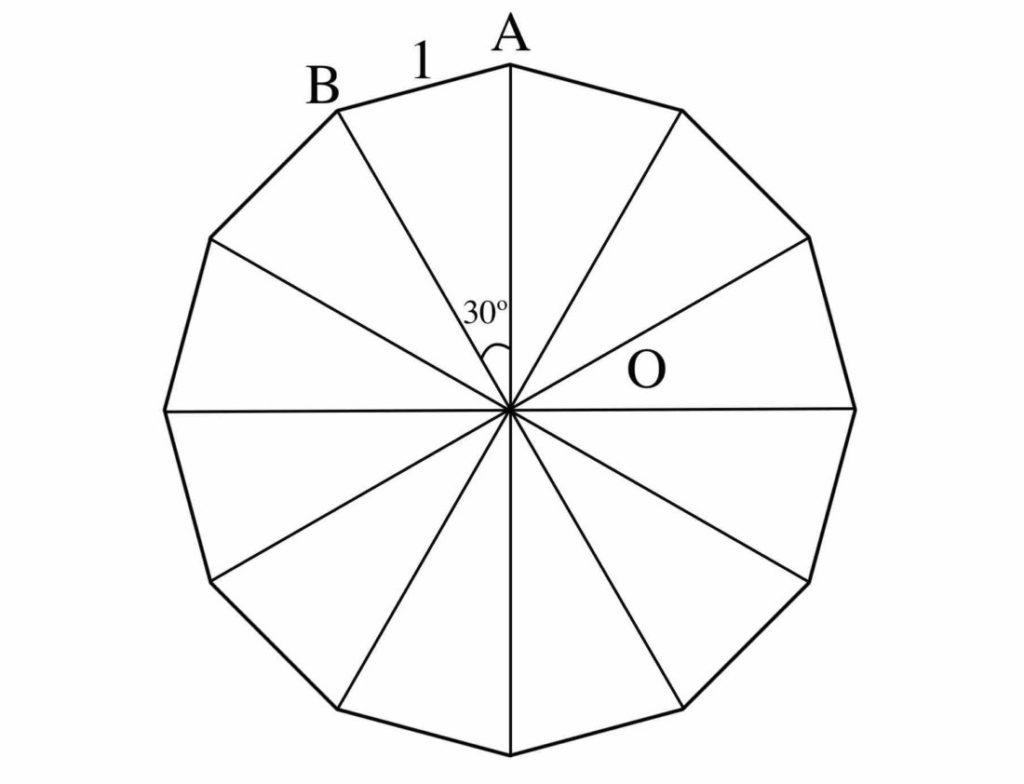



Jpdiamukpictz0dl Vers Le Haut 正12角形 書き方 正12角形 書き方



フラクタル自然数1の定義で可視化する正多角形の法則性 発想力教育研究所 素数誕生のメカニズム



黄金比矩形および内接正五角形 正十角形の描き方




いろいろな正多角形をかいてみよう 家庭学習レシピ



黄金比矩形および内接正五角形 正十角形の描き方
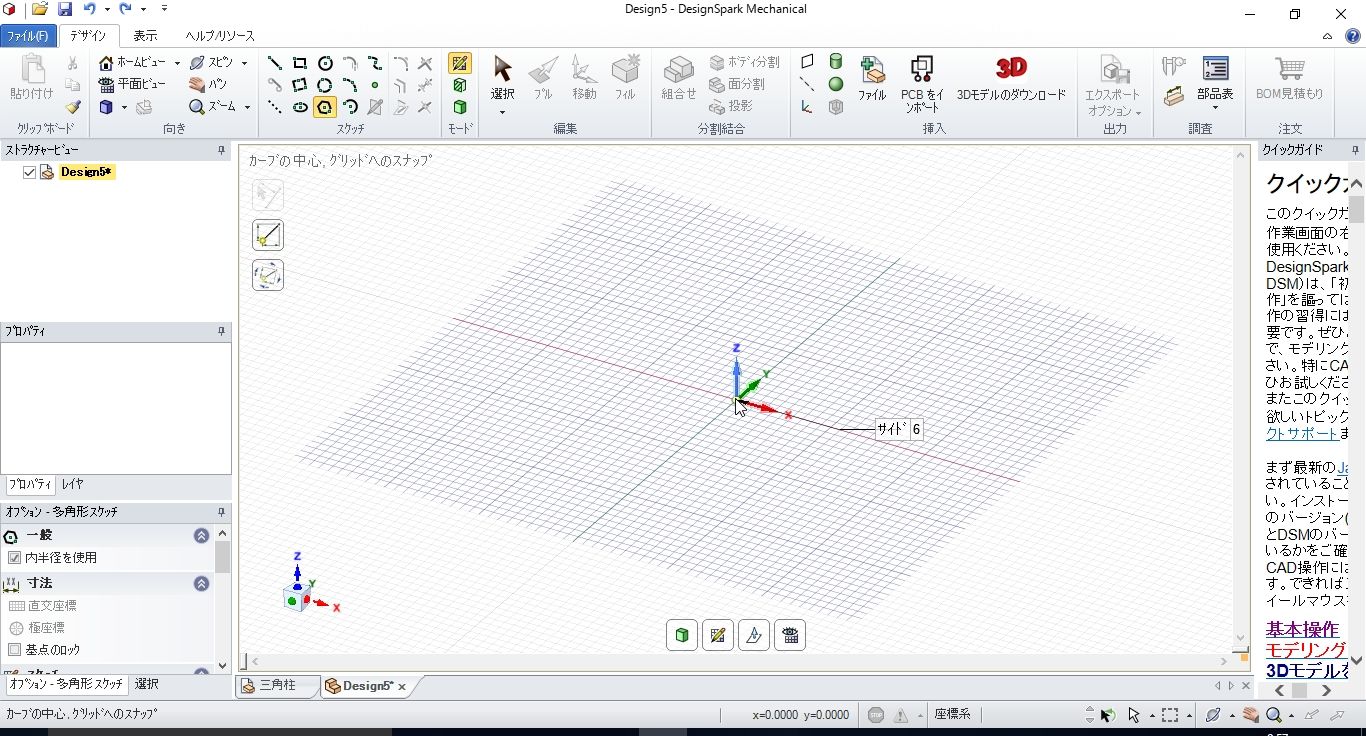



Designspark Mechanicalで基本図形 正多角形 パパは家族の長男 都会暮らしを楽しく生きたい
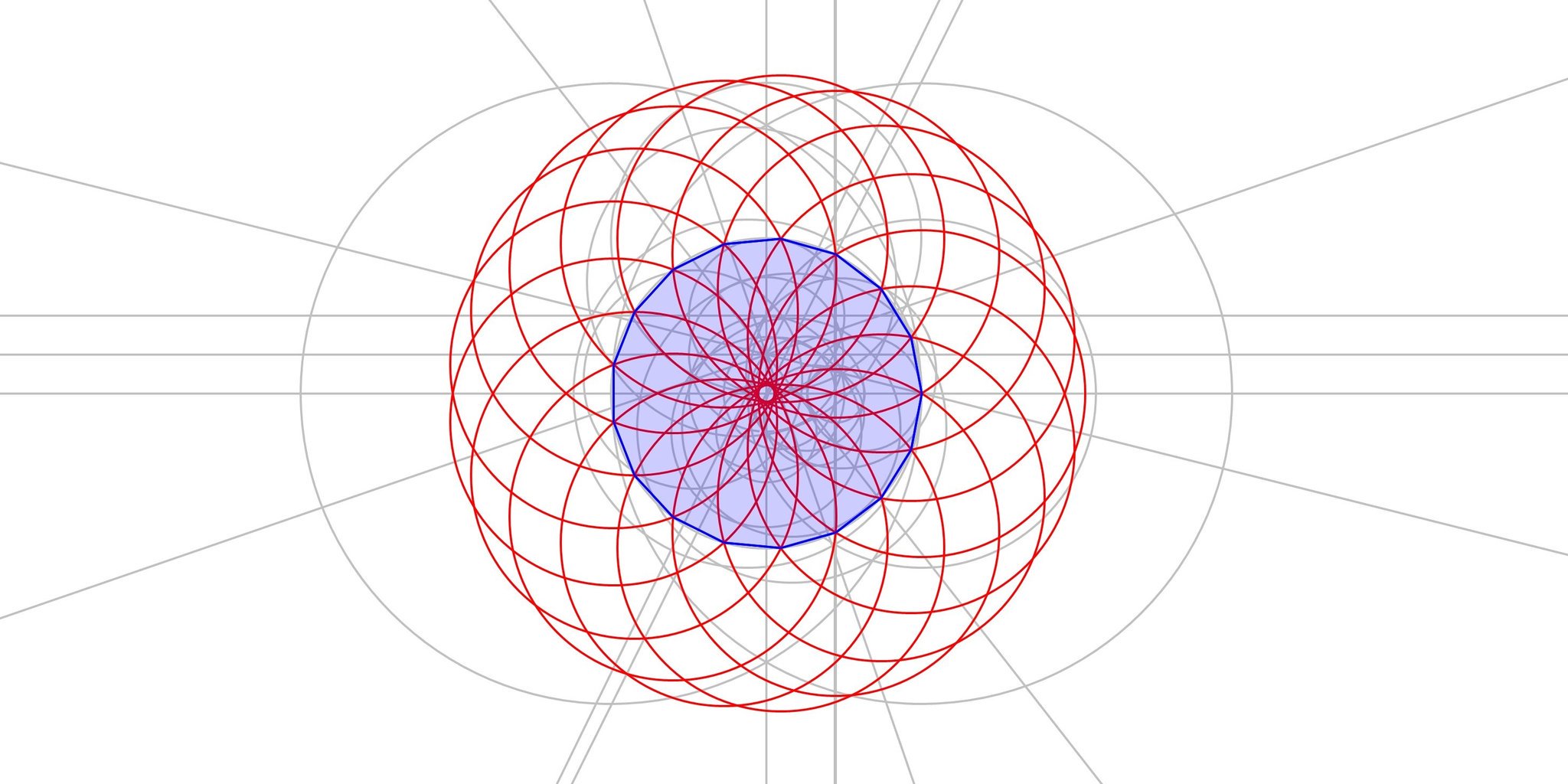



ポテト一郎 正十七角形 が作図出来ることは有名な事実であるが 実際に作図をするのはなかなかに大変な作業である 今までは見送っていたのだが 図形好きとして一度くらいは作図をしてみようかと思い立った 最後に頂点が次々と作図されるところは




Wo1999 号 製図用万能尺 Astamuse
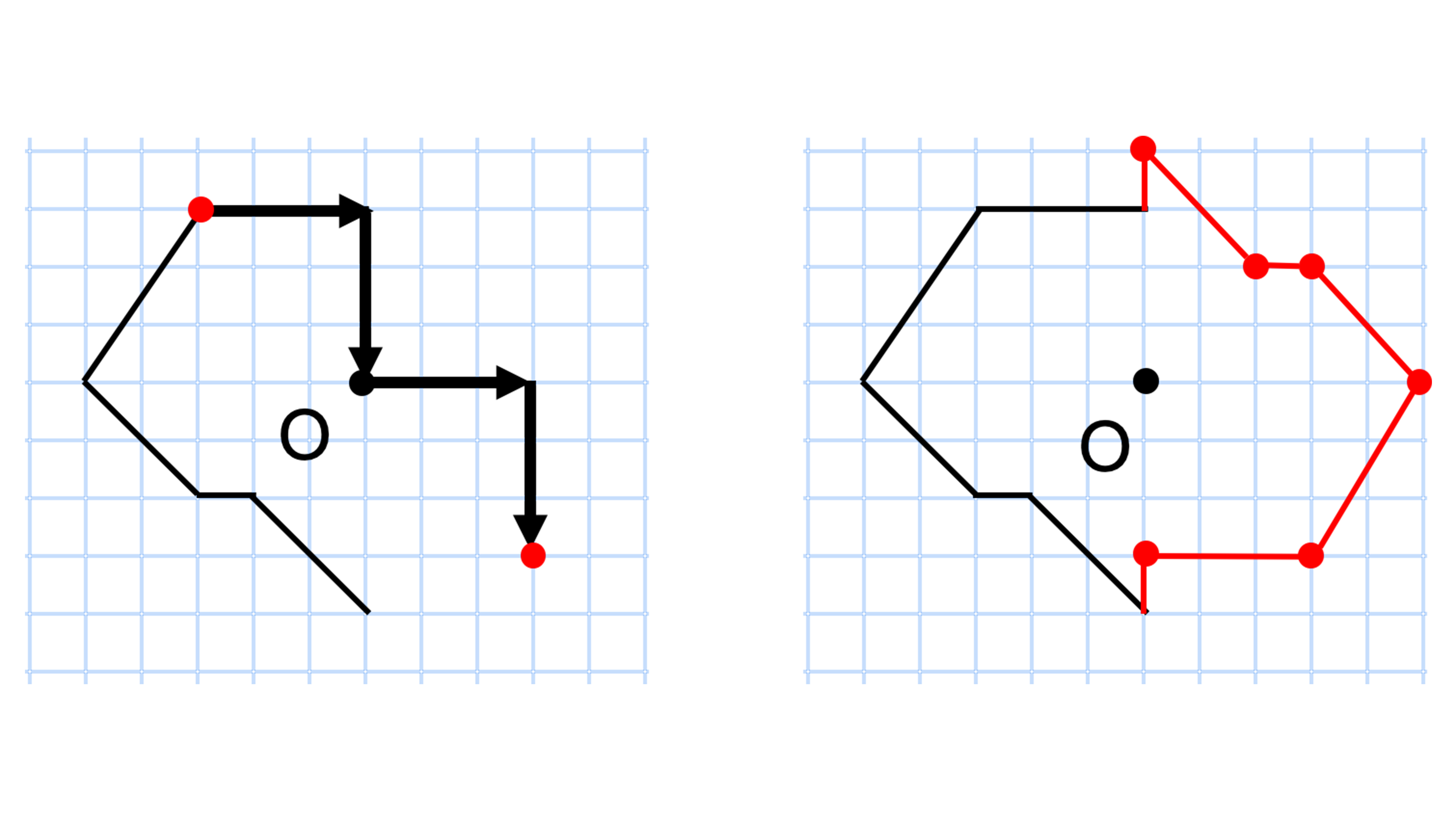



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




フラクタル自然数1の定義で可視化する正多角形の法則性 発想力教育研究所 素数誕生のメカニズム
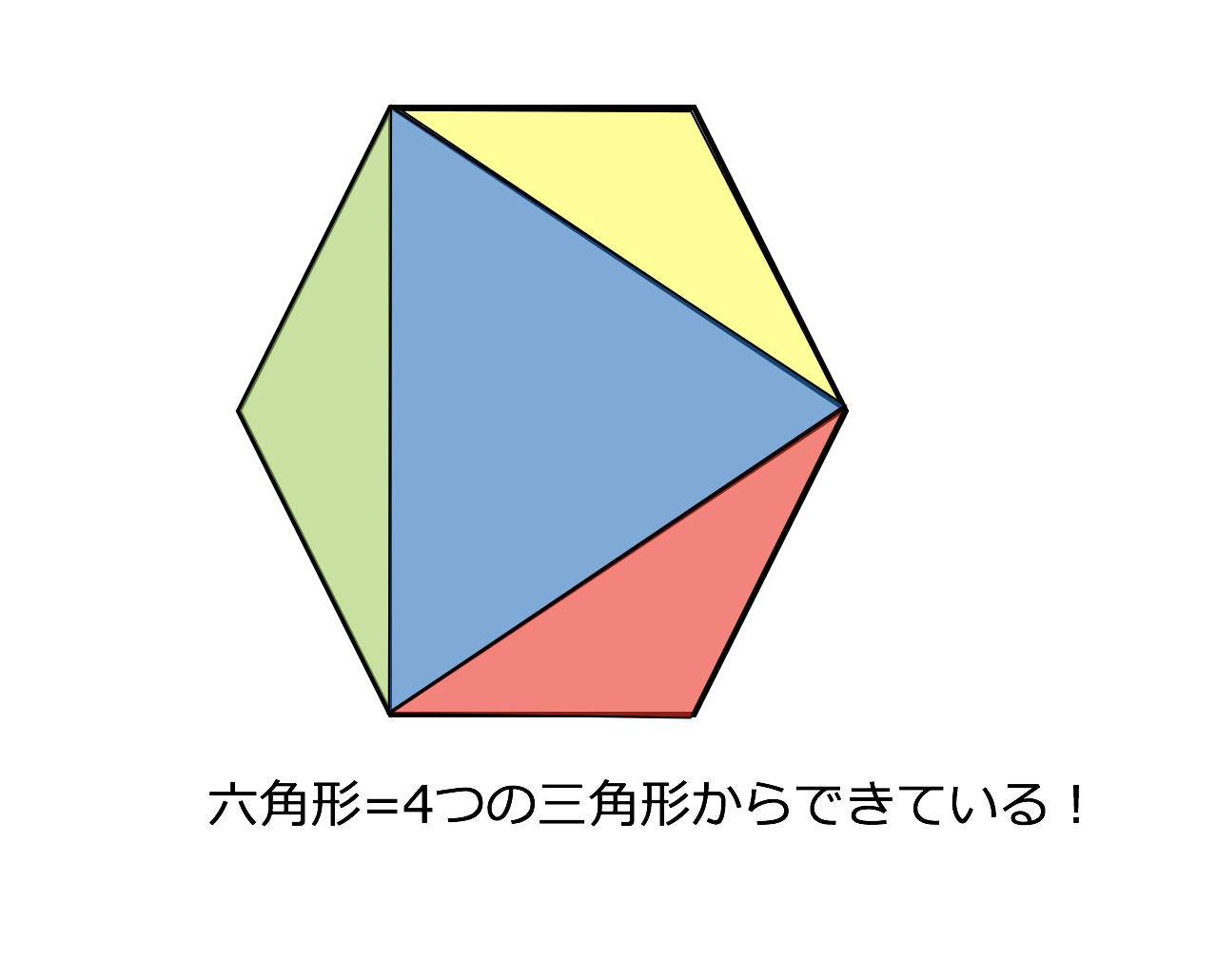



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
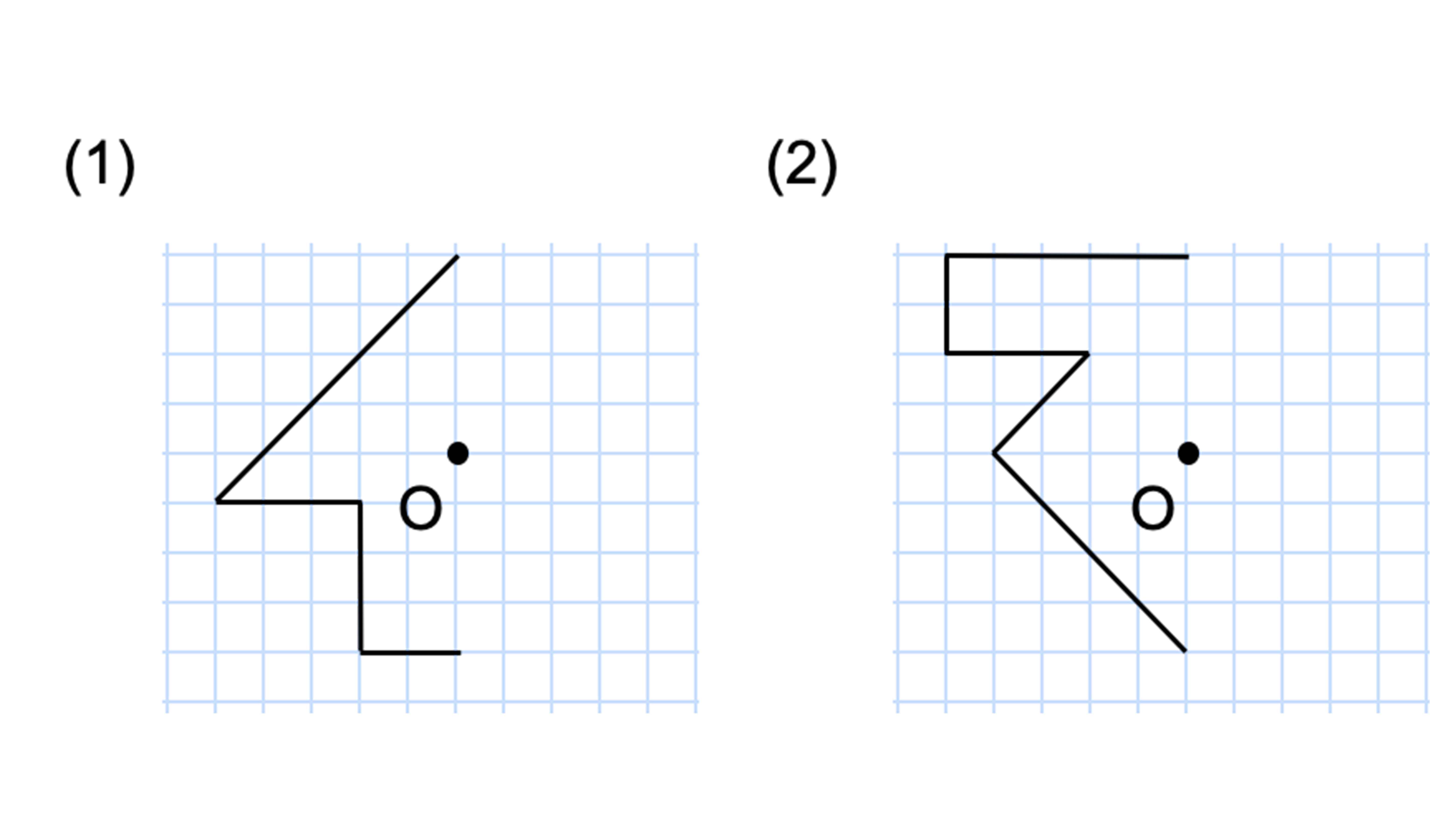



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
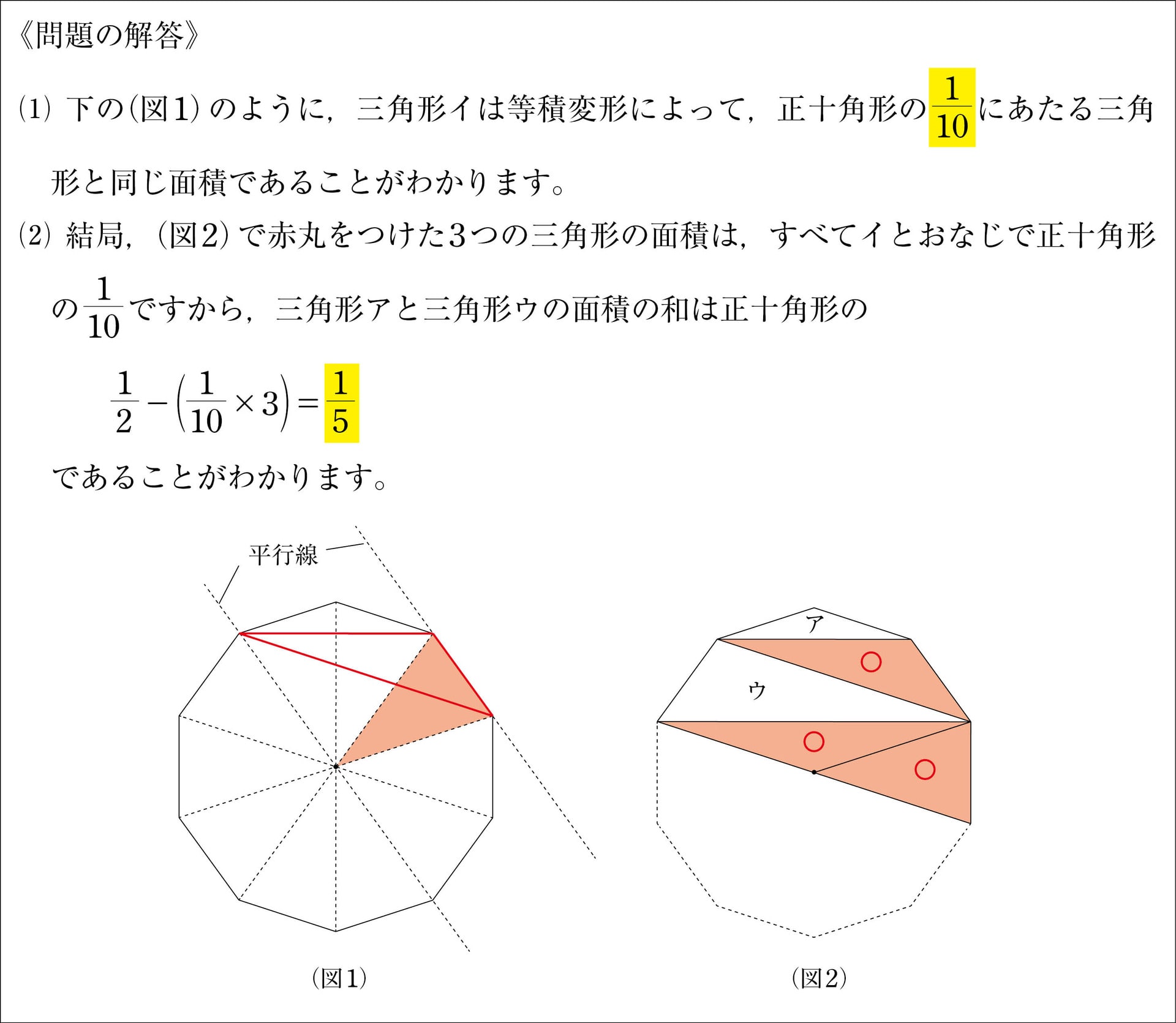



新鮮な正10 角形 最高のぬりえ
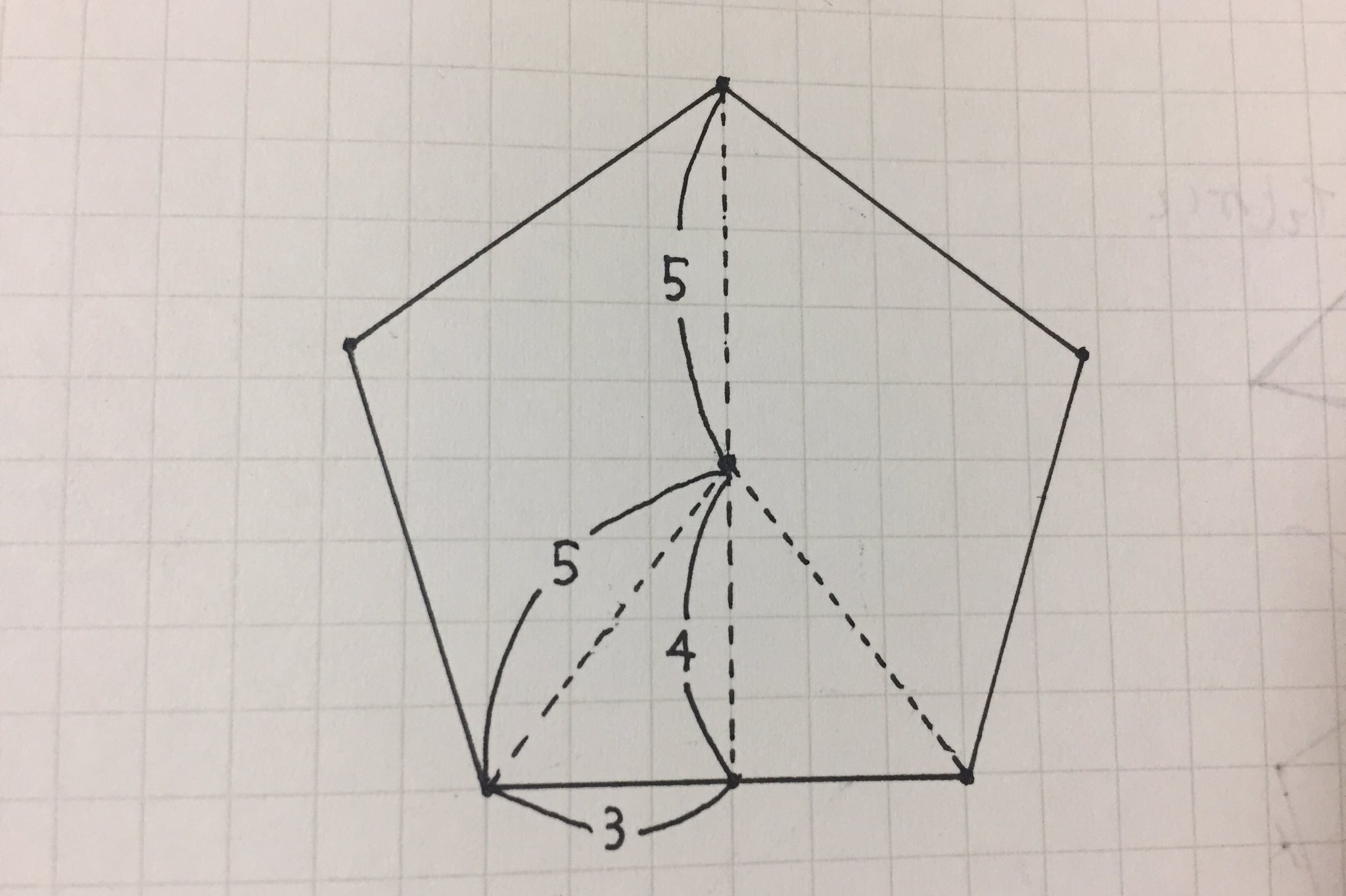



Askaboutmathp 方眼紙のマス目をいかして ほぼ 正五角形を描く描き方を考える過程で面白い事実に気づきました 中心点と頂点を結んでできる三角形は ほぼ ピタゴラスの三角形 3 4 5 を2つ組み合わせた形になります 今まで全く気が付きませんでした 意外な




小5 算数 小5 54 正多角形 Youtube



新鮮な正10 角形 最高のぬりえ
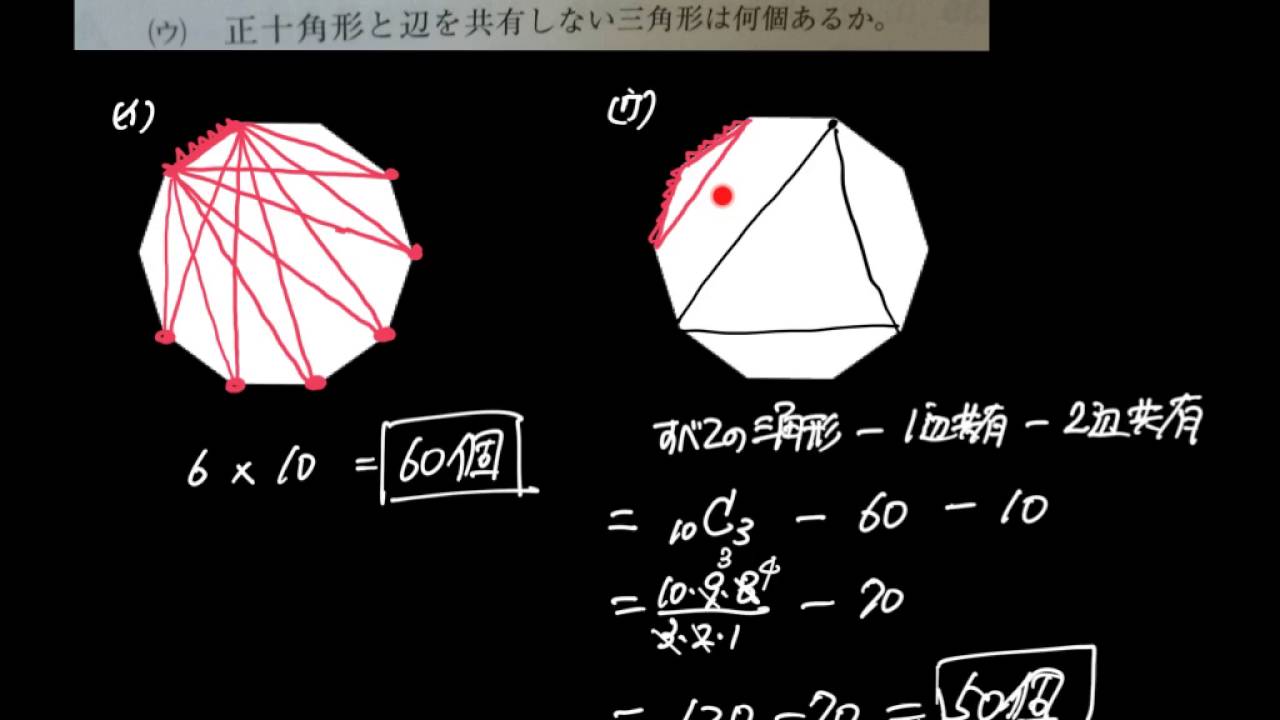



数a 正10角形 一辺を共有する三角形 Youtube




Ghly5u8wgqo16m
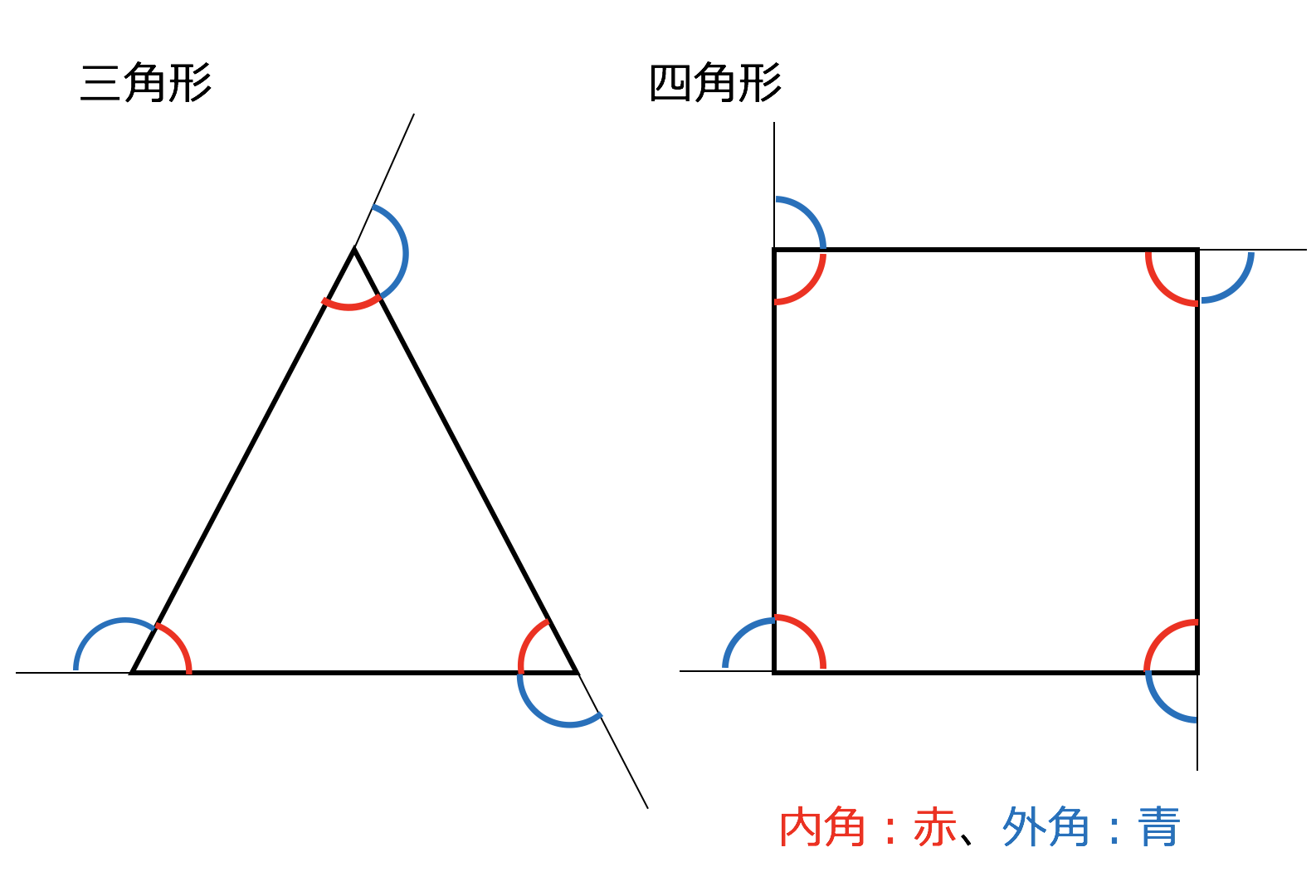



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




正多角形をプログラムを使ってかこう 杉並区立西田小学校 未来の学びコンソーシアム
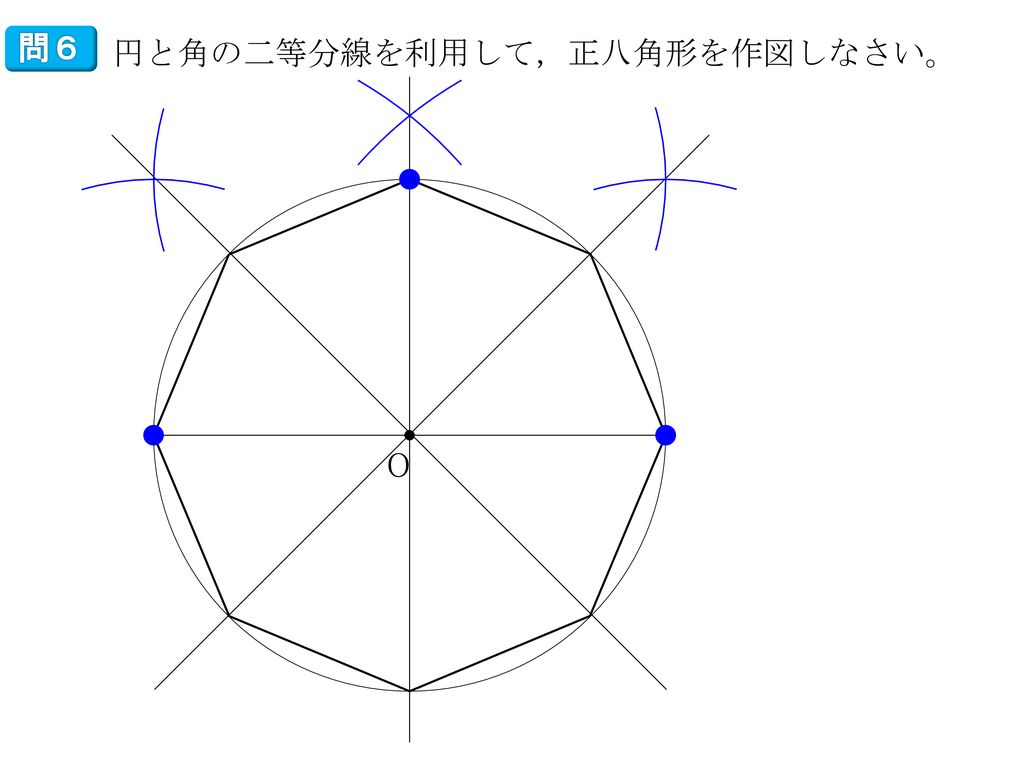



中学数学1年 5章 平面図形 2 作図 3時間 Ppt Download




コンパスで作図 正八角形の書き方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
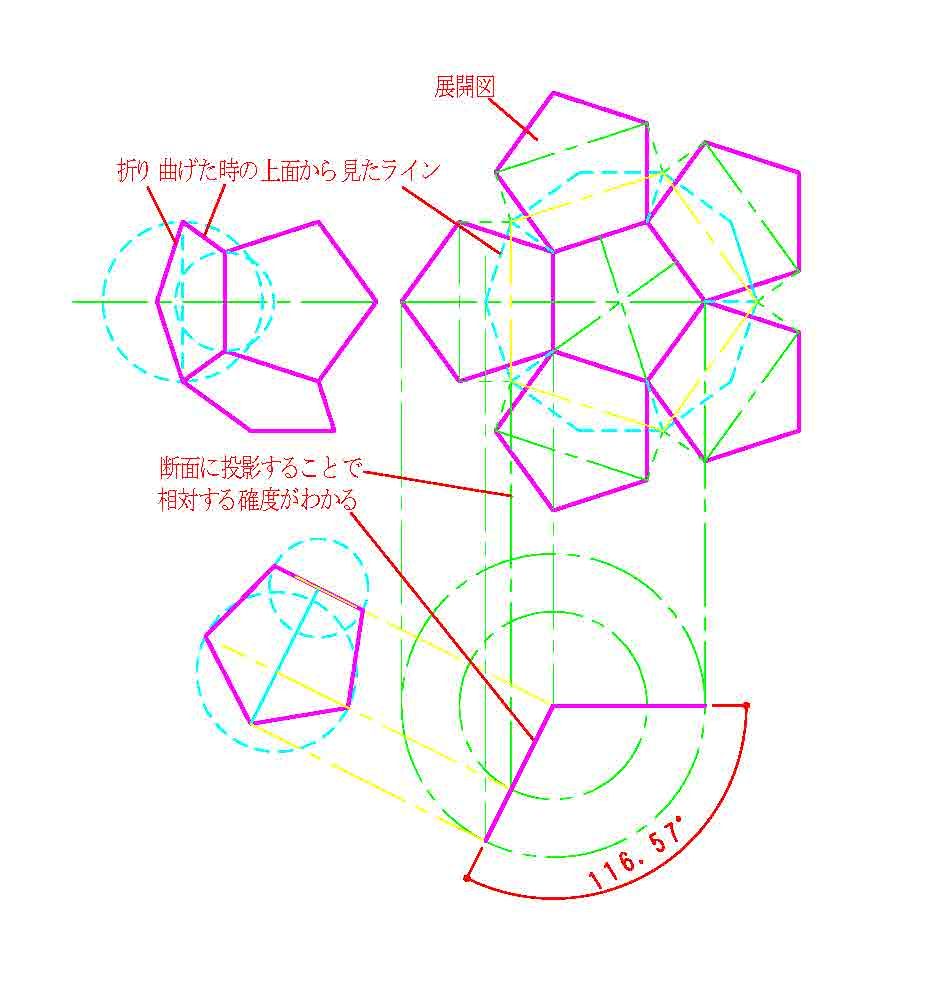



正十二面体のモデリングについて Autodesk Community International Forums
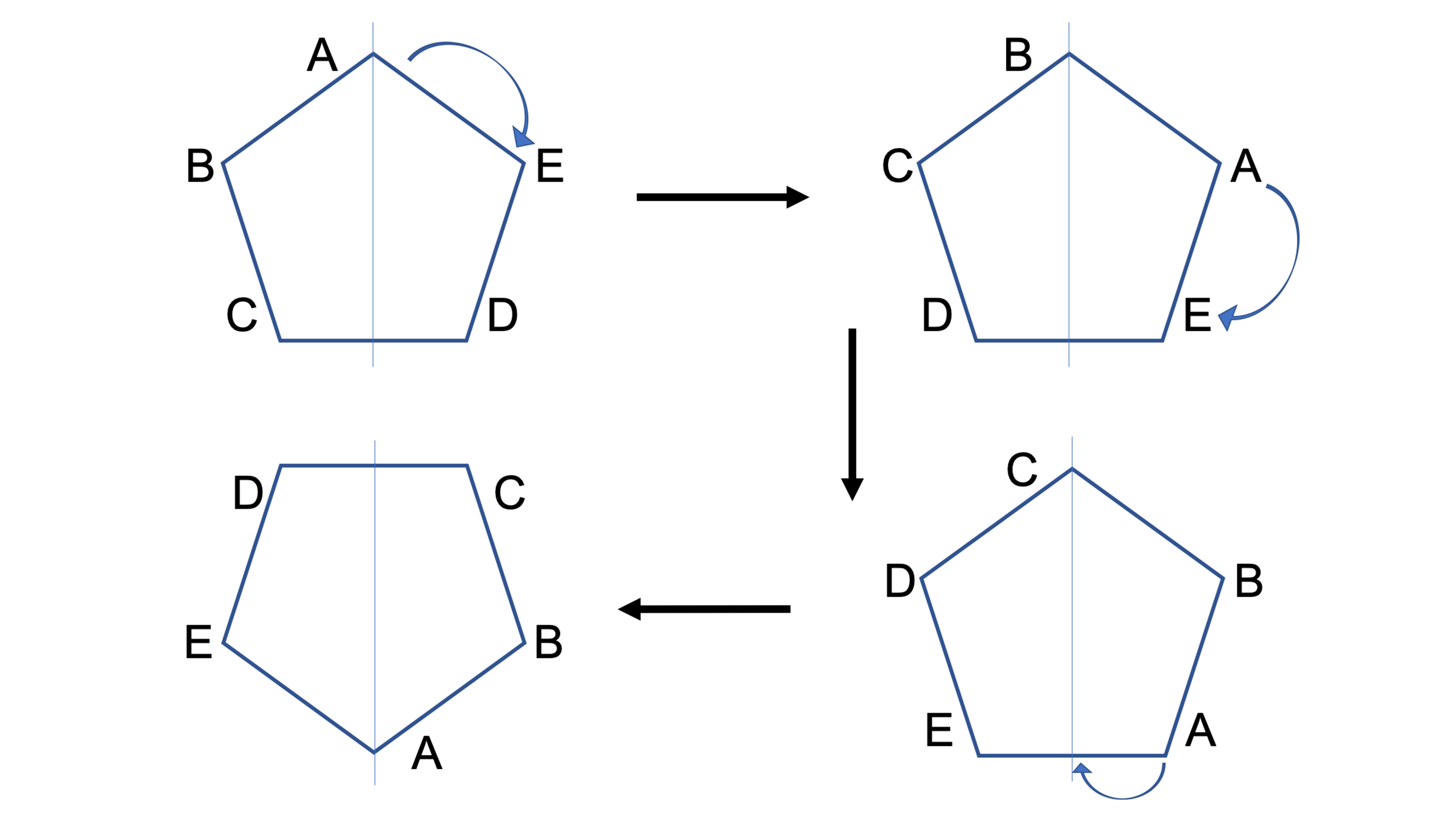



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




六角形を描く 3つの方法 Wikihow




解決済み 正八角形の書き方 ほぞの入れ方 Autodesk Community International Forums
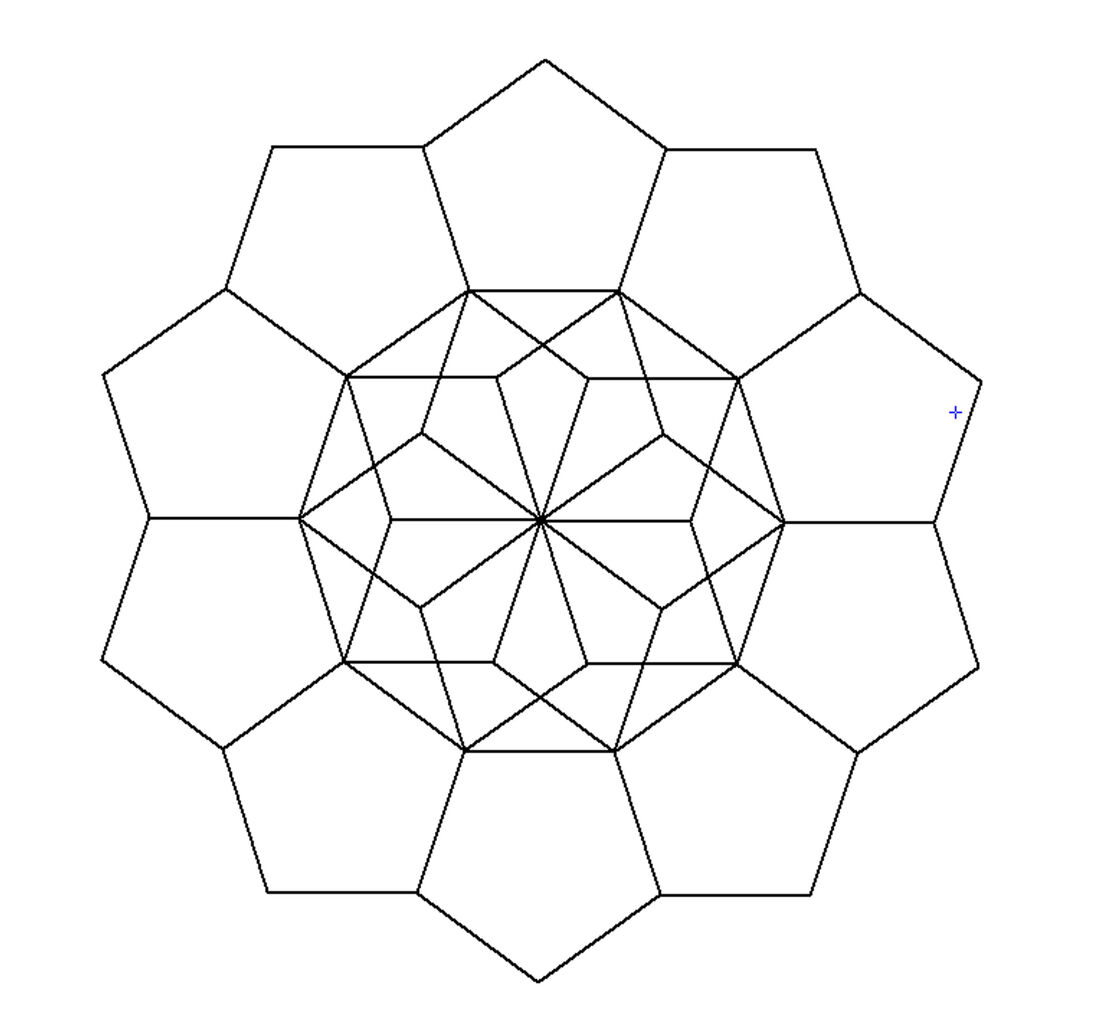



正5角形の積木箱 ペンタゴンデカゴンフラワー定理 倍角数定理 発想力教育研究所 素数誕生のメカニズム




高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月



0 件のコメント:
コメントを投稿